020

Protoże v§ak pro absolutni hodnotu komplcxniho ćisla z — a + b i plati

\z\ = \J a² + b²,

plyno odtud \z\ = d. Plati tedy:

Absolutni hodnota komplexiuho ćisla je rovna vzdalenosti jeho obrazu v Gaussove rovinć od poćatku soustavv souradnic.

Z tohoto geometrickeho vyznamu absolutni hodnoty komplexniho ćisla vyplyva, źe vśechna komplexni ćisla z, ktera maji touź absolutni hodnotu, vyplni v Gaussove rovine kruźnici se stredem v poćatku a s polomerem rovnym \z\. Pro komplexni jednotky, tj. pro komplexni ćisla z, pro neż je \z\ = 1, ma tato krużnice polomer jednotkoyy.

Priklad 1

V Gaussove rovine zobrazte vśechna komplexni ćisla, pro nćź plati

|1 + i| = \^z\ > |-

Restem

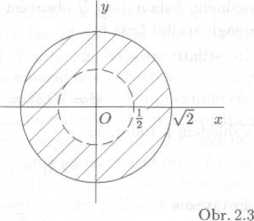
Vśechna komplexni ćisla z, pro neź je |s| > 5, vyplni vnejsek kruhu se stredein v poćatku a s polomerem Protoźe je dale |1 +i| = \/2, vyplni v§ech-na komplexni ćisla z, pro neź je |z| ^ |1 + i|, kruh se stredem v poćatku a s polomerem \/2. Komplexni ćisla z, ktera splńu-ji danou podminku

|1 + i| = \^z\ >

yyplni tedy tu ćast. Gaussovy roviny, ktera je prunikem obou tech-to oblasti (viz obr. 2.3); to, źe komplexni ćisla z, pro neź |z| = |, do tohoto pruniku nepatri, je znazorneno preruścvanou ćarou. Pozna-te z obr. 2.3, ktera realna ćisla a vyhovuji danemu vztahu? (Jsou to ćisla a e (-\/2, —5) U (5, \/2).)

Vśimneme si jeśte geometrickeho yyznamu absolutni hodnoty rozdilu komplexnich ćisel Z\, z₂, tj. yyrazu \z\ -2₂|. Oznaćime-li z\ = a + id, Z2 — c + di, dostaneme

|*i -z-ź\ = |(a + 6i) - (c + di)| =

= |(o — c) + (6 - d)i| = y/{a — c)² + (b — d)'².

Protoźe vśak yyraz \J{a — c)² + (b — d)² urćuje yzdalenost bodu [a, 6], [c, d\ a protoźe tyto body jsou obrazy komplexnich ćisel o + 6 i, c + di, znamena to, źe yyraz |z\ - z₂| urćuje yzdalenost komplexnich ćisel Z\, Z2 v Gaussove rovine.

Absolutni hodnota rozdilu komi>lexnich ćisel urćuje jejich vzda-lenost v Gaussovp rnvinć.

Pozndmka. Jestliźc ve vztahu d = |zi — z₂| pro vzajemnou yzdalenost d kom-plexm'ch ćisel zi, z₂ poloźlme 22 - 0, dostaneme d = |zi|, coz je nam uż znamy yysledek: yzdalenost d komplexnlho ćisla zi od poćatku je rovna jelio absolutni hodnote.

Priklad 2

V Gaussoye rovine zobrazte vśechna komplexni ćisla z, pro neź plati

\z-i\t |z + l- 2i|.

Reiśeni

Vyraz | z — i| urćuje yzdalenost komplexniho ćisla z od ćisla i a vy-raz \z + 1 — 2i| = \z — (—1 + 2i)| yzdalenost ćisla z od ćisla -1 + 2i.

39