022

2.4 Pomoci neroynosti mezi absolutnimi hodnotami komplexnich ći-sel yyjadrete vśechna komplexni ćisla z, ktera od kofene rovnice (1 — i)z — 2i = 0 maji

a)    vzdalenost vetśi neź 1 a menśi ncź 2,

b)    menśi yzdalenost neź od Cisla 1 + i.

*2.5 V Gaussove rovine zobrazte yśechna komplexni ćisla z, pro neź plati:

a)

b)

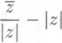
z — 1 — i

> |* + i|

= 1 a zaroveń

2.2 Goniometricky tvar komplexnflio ćisla

Komploxni ćisla jsme aź dosud zapisovali pouzo v algebraickem tvaru. Ukaźeme si nyni jiny zpusob jejich zapisu, tzv. goniometricky tvar komplexniho ćisla.

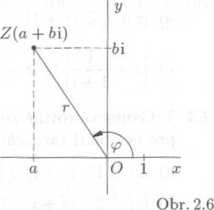
V Gaussove rovinć muźeine libovolny bod Z, ktery je obrazem komplexniho ćisla z = a + b\, urćit pomoci kartezske souradnicove soustavy Ozy tak, źe za ^-ovou souradnici tohoto bodu yezmeme real-nou ćast ćisla z a za y-ovou souradnici jeho ćast imaginarni. Je-li tento bod Z obrazem ćisla z = a + bi ^ 0, mużeme jej urćit i jinym zpiiso-bem, a to pomoci jeho vzdalenosti r od poćatku O a yelikosti orientova-neho uhlu tp, jehoź poćatecni raine-no je kladna poloosa z a koncove ra-rneno poloprimka OZ (viz obr. 2.6).

(Je zrejme, źe ćislo z = 0 pomoci ćisel r, <p yyjadfit nelze: bod Z to-tiź v tomto pripade spłynę s poćat-kem O a body O, Z pak neurćuji źadnou poloprimku, ktera by moh-la byt koncoyym ramenem oriento-yaneho uhlu.)

Realne ćislo (fi urćujici velikost tohoto orientovaneho uhlu se liazy va argument komplexniho ćisla z; z vlastnosti orientovaneho uhlu plyne: ma-li komplexni Cisło 2 / 0 argument <p, ma też argument <p + 2kr., kde k je libovolne cele ćislo. Nazev pro Cisło r zavadet. nemu-sime, nebot’ je jasne, źe je rovno absolutni hodnotC cisla 2, tj. r = \z\. Z obr. 2.6 je dale zrejme, że plati

b

a

sin <p = - , cos <fi — —

r

r

odkud pro ćislo 2 dostavame

z = a + bi = r cos fi -1- (r siny?)i — r(cosifi + isin<£>),

kde r — y/a² + b²; ffkame, że jsme ćislo 2 yyjadrili v goniometrickem tvaru.

Goniometricky tvar komplexniho Cisla 2 ^ 0 je jeho yyjadreni ve tvaru

2 = r(cos<^ + i sin >,?);

Cisło <p je argument komplexniho Cisla 2, r je jeho absolutni hodnota.

fi = i”, a protoże r — y/2, dostavame 2 = 1 + i = \pi (cos |x -I- i sin |it).

Nektera ćisla zapsana v algebraickem tvaru lze na tvar goniometricky prevest. velmi snadno, pokud je z jcjich umisteni v Gaussove rovine zrejmy jejich argument. Tak napr. ćislo 2 = 1 + i ma argument

Podobnym zpusobem dostaneme:

2 - 2i = 2\/2 (cos |x + i sin j7t) 3i = 3 (cos |x + i sin i u)

I = i (cos x + i sin x)    - i = cos §rc + i sin §x

Obecne pfi urćovani goniometrickeho tvaru komplexniho Cisla 2 = a + 6 i / 0 postupujeme takto: z yyjadreni

■)

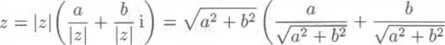
J

43