031

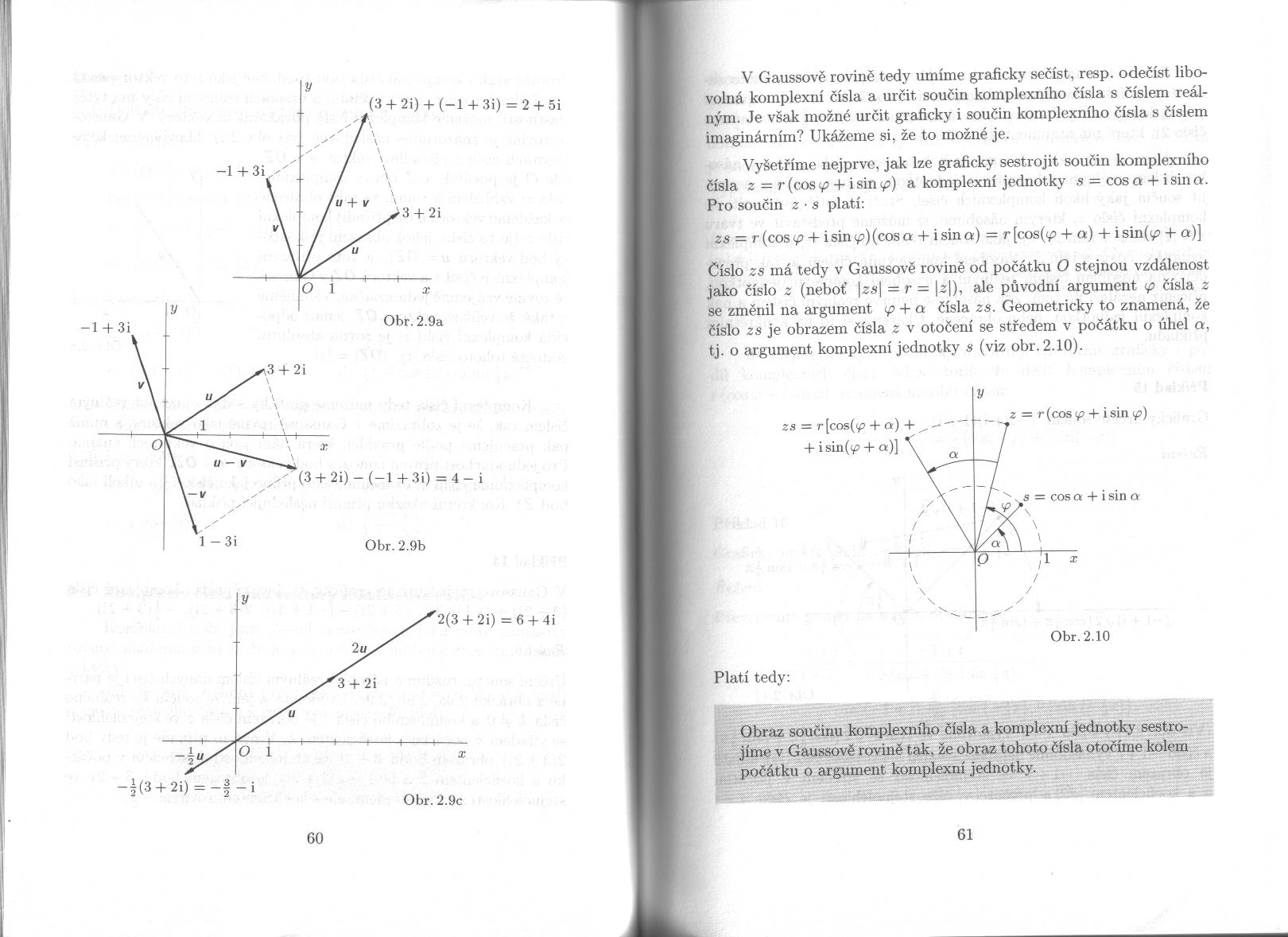
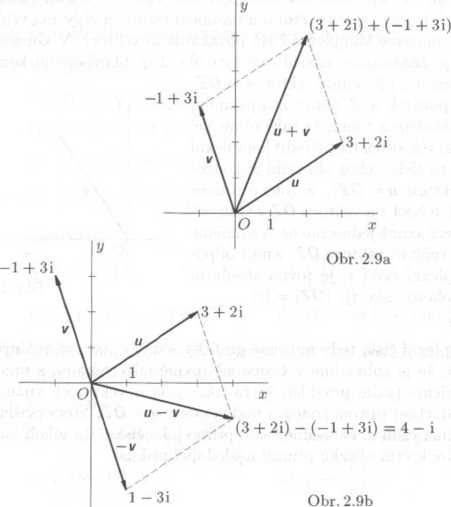
2 + 5i

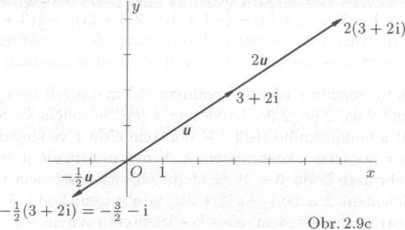
6 + 4i

V Gaussove rovine tedy umime graficky sećist, resp. odećist libo-volna komplexni ćisla a urćit soućin komplexniho ćisla s ćislem realnym. Je vsak możne urćit graficky i soućin komplexmho ćisla s ćislem imaginarnim? Ukażcme si, że to możne je.

Vyśetfime nejprve, jak lze graficky sestrojit soućin komplexniho ćisla z — r (cos ip + i sin ip) a komplexni jednotky .s - cos a + i sin a. Pro soućin z • s plati:

zs = r (cos ip + i sin v?) (cos a -I- i sin a) = r[cos(<p + a) + isin(v? + a)]

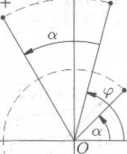
Cisło zs ma tedy v Gaussove rovine od poćatku O stejnou vzdalenost jako ćislo z (nebot’ |zs| = r — |z|), ale puvodni argument ip ćisla z se zmenil na argument <p + a ćisla zs. Geometricky to znamena, że ćislo zs je obrazem ćisla z v otoćeni se stredem v poćatku o uhel a, tj. o argument komplexni jednotky s (viz obr. 2.10).

y

zs = r [cos(</? + <*)■' + isin(<^ + a)]

s = cos o + i sin a

\

1 x

\

\

N.

z = r (cos ip + i sin p)

/

/

Obr. 2.10

Plat.i tedy:

Obraz soućinu koinplexniho ćisla a komplexni jednotky sestro-jime v Gaussovć rovinć tak, że obraz tohoto ćisla otoćime koleni poćśtku o argument komplexni jednotky.

61