021

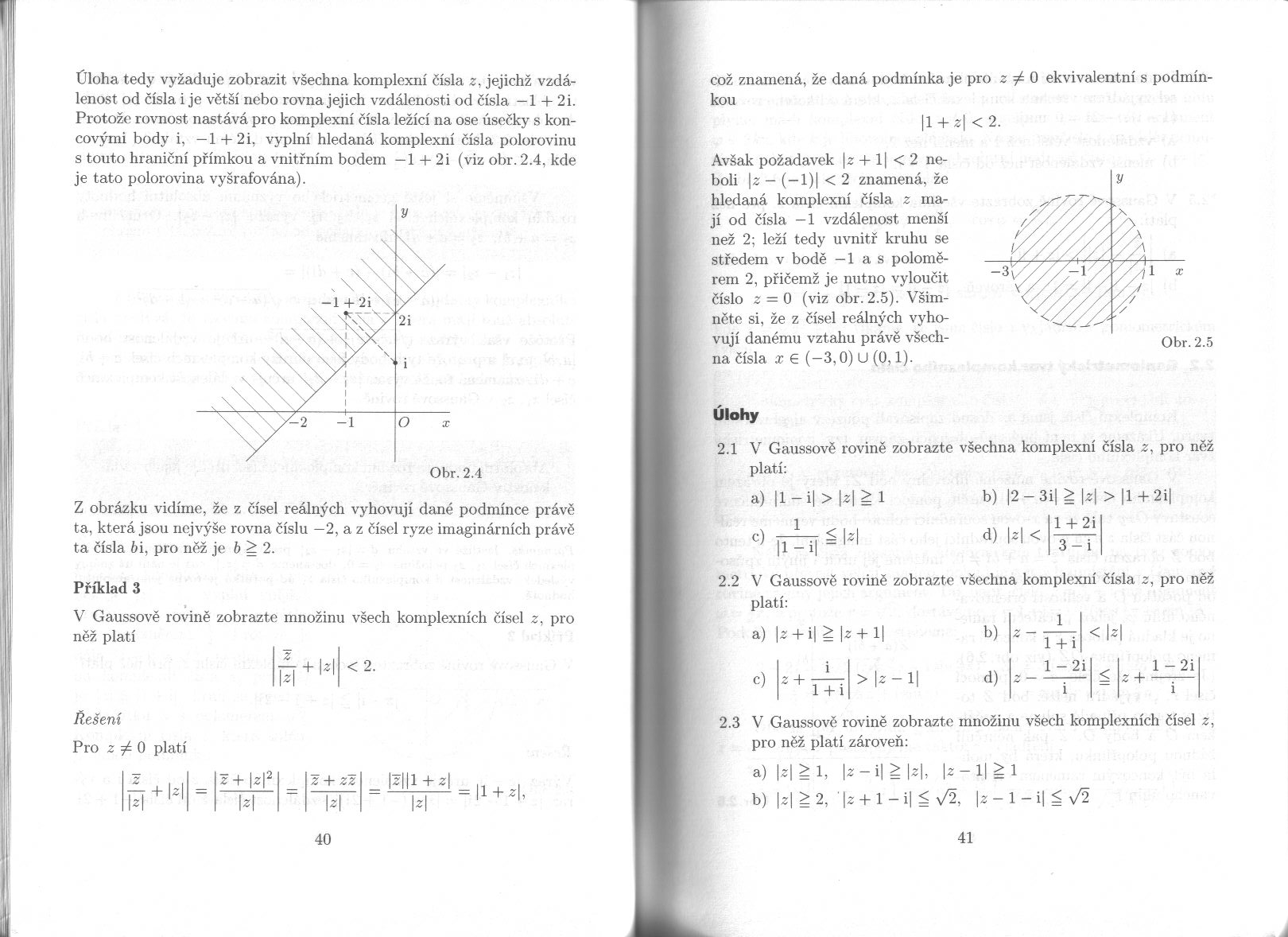
Uloha tedy vyźaduje zobrazit vśechna komplexni ćisla z, jejichż vzda-lenost od ćisla i je vćtsi nebo rovna jej ich vzdalenosti od ćisla -1 + 2 i. Protoże rovnost nastava pro komplexni ćisla leżici na ose usećky s końcowymi body i, — 1 + 2i, vyplni hledana komplexni ćisla polorovinu s touto hranićni primkou a vnitfnim bodem —1 + 2i (viz obr. 2.4, kde je tato polorovina vysrafovana).

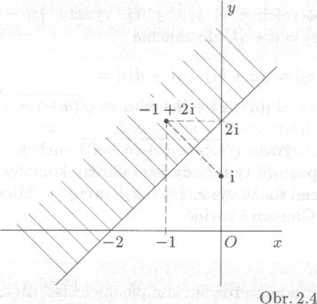
Z obrazku vidime, źe z ćisel realnych vyhovuji dane podmince prave ta, ktera jsou nejvy§e rovna ćislu —2, a z ćisel ryzę imaginarnich prave ta ćisla bi, pro neż je b ^ 2.

Priklad 3

V Gaussove rovine zobrazte rrmoźinu vśech komplexnich ćisel z, pro neź platl

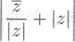
< 2.

Reseni

Pro 2/O plati

ż+NI²

NI

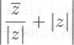
z + zz

“ŃT

\m+z\

NI

1 + z\,

coż znamena, źe dana podminka je pro z ^ 0 ekvivałentm s podmin-kou

\l + z\< 2.

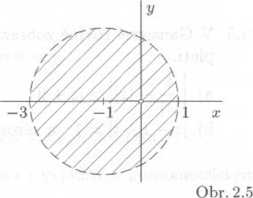
Avsak poźadavek \z + 1| <2 ne-boli \z — (—1)| < 2 znamena, że hledana komplexni ćisla 2 ma-ji od ćisla —1 vzdalenost menśi neź 2; leżi tedy uvnitr kruhu se stredem v bodę —las polome-rem 2, prićemź je nutno vyloućit Cisło 2 = 0 (viz obr. 2.5). Vśim-nćtc si, źe z ćisel realnych vyho-vuji danemu vztahu prave vsech-na ćisla x € (-3,0) U (0,1).

Ulołiy

2.1 V Gaussove rovine zobrazte vśechna komplexni ćisla z, pro neź piat, i:

a) |1 - i| > \z\ Z 1    b) |2 — 3i| ^ \z\ > |1 + 2i|

1    ^    „ , .    1 +2i

c)

11-

d) \z\ <

3 — i

2.2 V Gaussove rovine zobrazte v§echna komplexni ćisla 2, pro neź plati:

a) \z + i| ^ \z + 1|    b)

2 —

c)

z -f-

1 + i

> \z - 1|

d)

1 + i 1 — 2i

< \z\

<	1 — 2i
	Z + ;
	1

2.3 V Gaussovć rovine zobrazte innoźinu v§ech komplexnich ćisel 2, pro neź plati zaroveń:

a) 121 ;> 1, \z i| = \z\, \z - 1| ^ 1

b) \z\ ^ 2, |z + 1 -i| ^ V2, \z - 1 - i| ^ V2

i

41