040

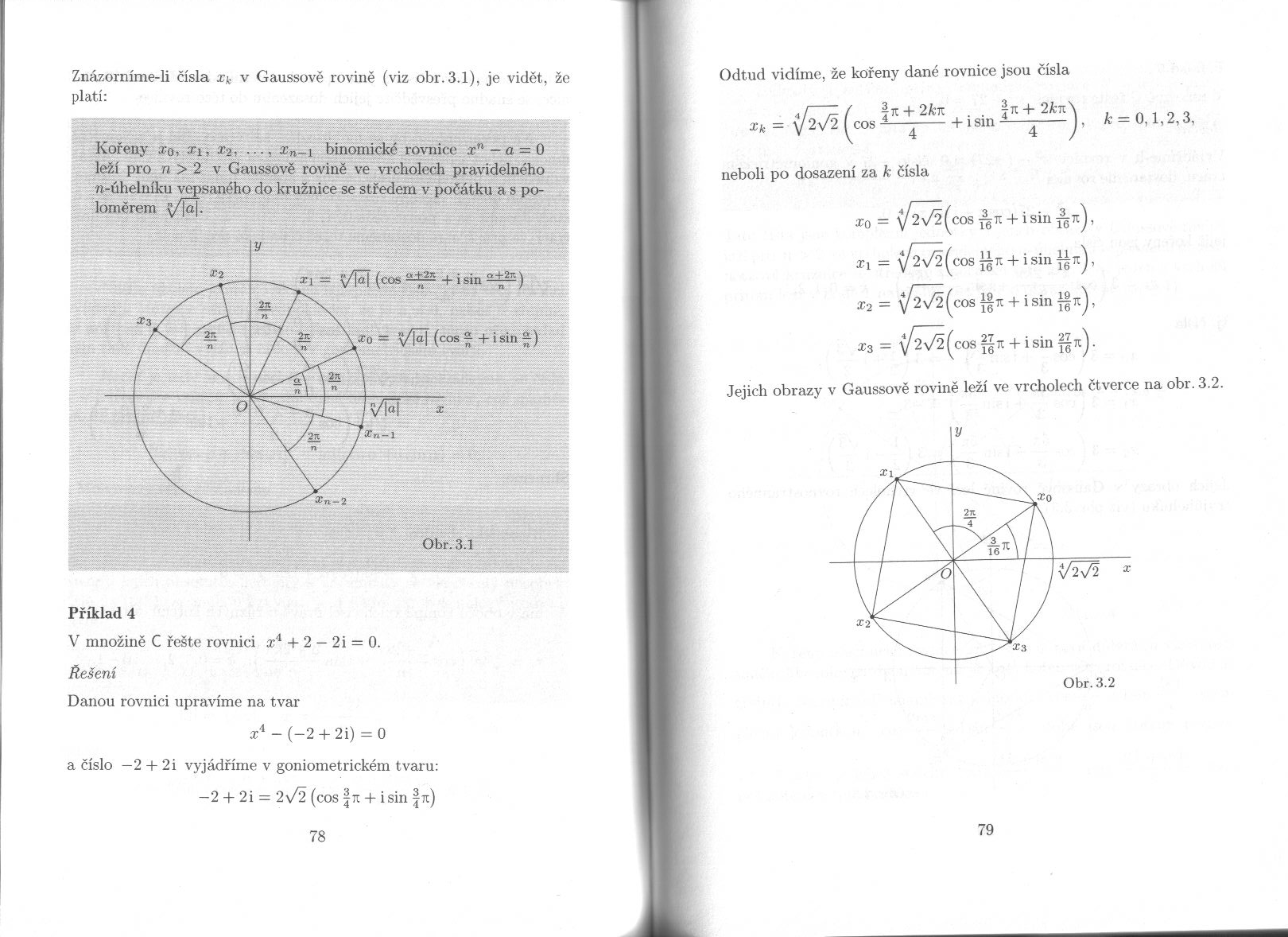
Znazornime-li dsla x\. v Gaussove rovine (viz obr.3.1), je videt, £e plati:

Koreny x₀, zi, x₂, .... x_n-i binomicke roviiice x" - o = 0 leźi pro n > 2 v Gausspye rovine ve vrcholech pravidelneho n-uhelnlku vepsaneho do krużnice se stfedem v podśtku a s po-

lomerem ^/jo|.
	y _= v/R (cos + isin
X3 / A--	2tc /
Ay 2n \ / ^n \	7^21 \ XO = ^/jof (^cos n + ‘ ^sin ^
	77 \ | « |
---Jb
	\ /2rt y^n-l
	Obr.3.1

Pfiklad 4

V mnożine C feśte rovnici z⁴ + 2 — 2 i = 0.

Reśeni

Danou rovnici upravime na tvar

z⁴ -(-2 + 2i) = 0

a ćislo —2 + 2i vyjadnme v goniometrickem tvaru: —2 + 2i = 2\/2 (cos frc + isin fit)

Odtud vidime. że koreny dane rovnice jsou ćisla

Xk

= V 2\/2

fjt + 2ku . . |n + 2kn

+1 sm

Ar = 0,1,2,3,

neboli po dosazeni za k ćisla

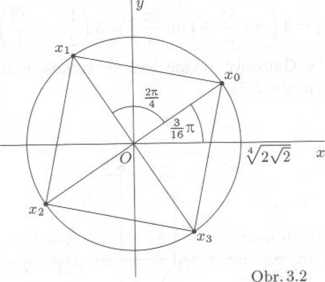
ar₀ =    >^2 72 (cos + isin

ar! =    \]272 (cos + i sin y±7i) ,

x2 =    \J272 (cos i§Tc + i sin    ,

ar₃ =    V^(cos fgTC + i sin    .

Jej ich obrazy v Gaussove rovine leżi ve vrcholech ćWerce na obr.3.2.

79