0173

175

S 2. Pole i objętość

wyżej. Przez d oznaczymy najdłuższą z przekątnych prostopadłościanów, na które został podzielony prostopadłościan W.

3) Bryła V ma objętość wtedy i tylko wtedy, gdy dla d-* 0 objętości \ X*\ i | Y*| dążą do wspólnej granicy \ V\. Jeśli spełniony jest ten warunek, to wspomniana granica daje objętość bryły V.

Dowody tych wszystkich twierdzeń pozostawiamy czytelnikowi; łatwo je skopiować z rozumowań z ustępu 336.

341. Klasy brył mających objętości. Podobnie jak w przypadku pola, istnienie objętości bryły V zależy całkowicie od własności brzegu S tej bryły. Jedno z kryteriów istnienia objętości [porównaj 338] brzmi następująco: na to, aby bryła V miała objętość, potrzeba i wystarcza, żeby jej brzeg S miał objętość 0, tzn., żeby można było ten brzeg umieścić w bryle wielościennej o dowolnie małej objętości.

Do powierzchni, których objętość jest równa 0, należą przede wszystkim powierzchnie mające równania jednej z trzech postaci

z = /(*> y) y = 9 (x, z) lub x = h (y, z),

gdzie funkcje/ g i h są funkcjami ciągłymi dwóch zmiennych, określonymi w pewnych obszarach ograniczonych.

Przypuśćmy na przykład, że dane jest równanie typu pierwszego w obszarze P, zawartym w prostokącie R. Na mocy twierdzenia z ustępu 174 dia każdego e > 0, można rozbić ten prostokąt na tak małe prostokąty R_t(i — 1, 2,..., ri), żeby oscylacja funkcji / w tej części P, obszaru P, która jest zawarta w R_t, była mniejsza od e/R. Jeśli m, i M_t oznaczają najmniejszą i największą wartość funkcji / w obszarze P_h to cała nasza powierzchnia leży w wielościanie złożonym z prostopadłościanów, których pola podstaw są równe R_t, a wysokości wynoszą co, = M_t—m_t. Objętość tego wielościanu jest równa

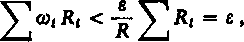
co należało udowodnić.

A więc, jeśli bryła V jest ograniczona kilkoma powierzchniami ciągłymi, z których każda z osobna ma równanie jednego z trzech podanych wyżej typów, to bryła ma objętość.

Aby sformułować stosowany zazwyczaj w praktyce szczególny przypadek tego kryterium, wprowadzimy pojęcie powierzchni gładkiej.

Niech powierzchnia będzie określona równaniami parametrycznymi

x = <p(u,v), y = y>(u,v), z = x(u,v),

gdzie funkcje q>, y>, x są ciągłe i mają ciągłe pierwsze pochodne cząstkowe w pewnym Ograniczonym i domkniętym obszarze na płaszczyźnie uv. Przyjmujemy, że brzeg L tego obszaru składa się z krzywych gładkich. Załóżmy wreszcie, że na powierzchni tej nie ma ani punktów wielokrotnych, ani w ogóle punktów osobliwych. Jeśli spełnione są wszystkie te warunki, to powierzchnia nazywa się gładka.