0175

177

§ 2. Pole i objętość

Jeśli zrzutujemy (bez deformacji) dwa takie przekroje na jakąkolwiek płaszczyznę prostopadłą do osi x, to rzuty te mogą być zawarte jeden w drugim (jak na rys. 27 a)) albo częściowo zachodzić na siebie (rys. 27 b)), albo wreszcie mogą leżeć jeden na zewnątrz drugiego (rys. 27 c)).

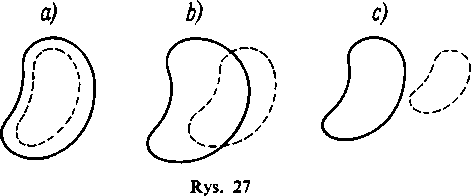
Zatrzymamy się najpierw na przypadku, kiedy rzuty na płaszczyznę prostopadłą do osi x dwu różnych przekrojów są zawsze zawarte jeden w drugim.

Przy tym założeniu twierdzimy, że bryła V ma objętość, wyrażającą się wzorem

b

(15)    \V\ = f\P(x)\dx.

a

Dla dowodu rozbijamy przedział <cr, ó> osi x na podprzedziały punktami a — x₀ < Xi < ... < x₍ < x,+! < ... < x_n = b,

a całą bryłę rozcinamy na warstwy płaszczyznami x = x_t poprowadzonymi przez te punkty podziału. Rozpatrzymy i-tą warstwę zawartą między płaszczyznami x = i x = x,₊₁ (i = 1, 2, n— 1). Funkcja \P (jc)| przyjmuje w przedziale <x,-, x_i+1> wartość największą M_t i najmniejszą m_t. Jeśli wszystkie przekroje odpowiadające różnym wartościom zmiennej x z tego przedziału zrzutujemy na jedną płaszczyznę, np. na płaszczyznę x = X(, to — przy przyjętym założeniu — wszystkie te przekroje leżą wewnątrz największego z nich, którego pole wynosi M_t, i zawierają przekrój o najmniejszym polu m_i. Jeśli na najmniejszym i największym przekroju zbudujemy dwa walce proste o wysokości Ax_t = = *,+!—x_t, to większy z nich zawiera całkowicie rozpatrywaną warstwę bryły, a mniejszy jest zawarty w tej warstwie. Na podstawie uwagi podanej na początku, objętości tych walców są równe odpowiednio M, Ax, i m_t Ax_t.

Walce zawarte w kolejnych warstwach tworzą bryłę T, a walce obejmujące te warstwy — bryłę U; objętości tych brył są równe odpowiednio

Y_JM_iAx_l i m_t Ax_t

t    i

i gdy X = max Ax_L dąży do zera, to sumy te mają wspólną granicę równą całce (15). Na mocy twierdzenia 2) z ustępu 340 taka sama jest objętość bryły V (¹).

Ważny przypadek szczególny, w którym spełnione są wskazane wyżej założenia o wzajemnym położeniu przekrojów, stanowią bryły obrotowe. Wyobraźmy sobie na

O Dzieląc na przykład przedział na równe części łatwo można otrzymać ciągi brył zawarte w bryle V i zawierające ją, o których jest mowa w cytowanym twierdzeniu.

12 RachnriAlr rMni/ivlr/v