0267

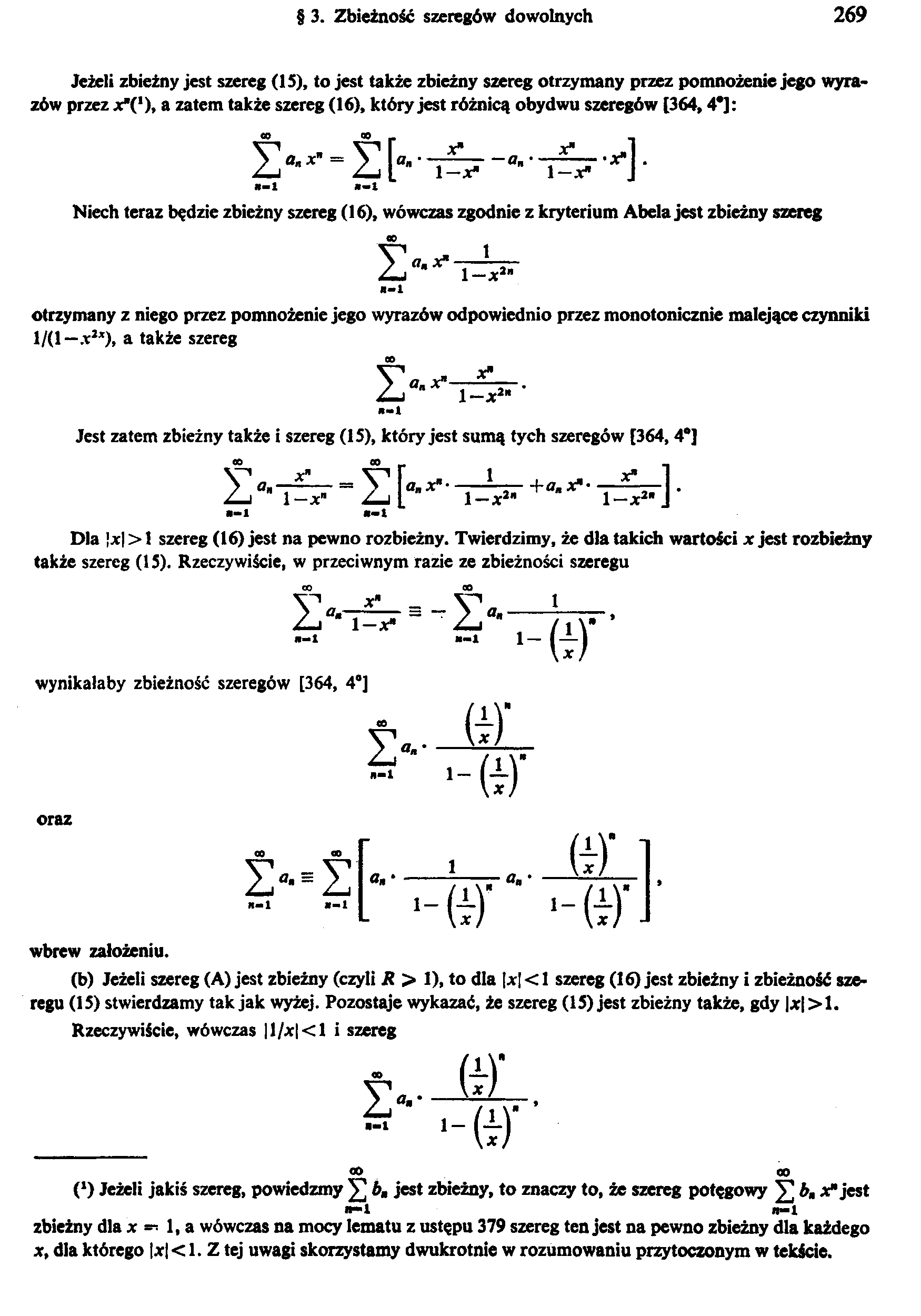
269

§ 3. Zbieżność szeregów dowolnych

Jeżeli zbieżny jest szereg (15), to jest także zbieżny szereg otrzymany przez pomnożenie jego wyrazów przez x^{1 2}(‘), a zatem także szereg (16), który jest różnicą obydwu szeregów [364,4²]:

CO

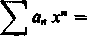
8-1

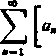
JC*

1-X-

y

l-y

•y

i-

Niech teraz będzie zbieżny szereg (16), wówczas zgodnie z kryterium Abela jest zbieżny szereg

00

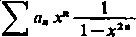
8—1

otrzymany z niego przez pomnożenie jego wyrazów odpowiednio przez monofonicznie malejące czynniki 1/(1—x^lx), a także szereg

V a.²"—

Z-j l-x²"

8—1

Jest zatem zbieżny także i szereg (15), który jest sumą tych szeregów [364,4°]

y a,—— = y [a.²"--+«„x"--£_|.

Z_i    1 —xⁿ    Z_iL ’    l-x²"    l-x²"J

8-1    8-1

Dla |x| > 1 szereg (16) jest na pewno rozbieżny. Twierdzimy, że dla takich wartości x jest rozbieżny także szereg (15). Rzeczywiście, w przeciwnym razie ze zbieżności szeregu

oo    co

kr

- '-(t)

wynikałaby zbieżność szeregów [364, 4°]

oraz

oo ao

I-E

8—1 8—1

- -(²)

JźL

-(i)'    -(7)'

wbrew założeniu.

(b) Jeżeli szereg (A) jest zbieżny (czyli R > 1), to dla [x[ < 1 szereg (16) jest zbieżny i zbieżność szeregu (15) stwierdzamy tak jak wyżej. Pozostaje wykazać, że szereg (15) jest zbieżny także, gdy |jc| > 1. Rzeczywiście, wówczas |l/x|<l i szereg

8-1 1-

1

00    00

2

Jeżeli jakiś szereg, powiedzmy b. jest zbieżny, to znaczy to, że szereg potęgowy    b, x²jest

w-l    n-l

zbieżny dla x =-■ 1, a wówczas na mocy lematu z ustępu 379 szereg ten jest na pewno zbieżny dla każdego x, dla którego |x| < 1. Z tej uwagi skorzystamy dwukrotnie w rozumowaniu przytoczonym w tekście.