0268

270

XI. Szeregi nieskończone o wyrazach stałych

jak wspomnieliśmy jest zbieżny, a zatem jest także zbieżny [374,4°] szereg

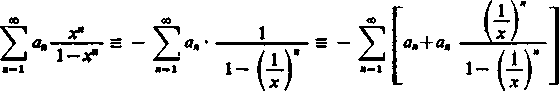
6) Na zakończenie, jako przykład bezpośredniego zastosowania przekształcenia Abela (10), podamy tożsamość

£    •*" = U ~ x)    A. x",

B-l    «-l

gdzie

A, = O0+O1+    +o»    (« = 0, 1, 2, ...).

Zakładamy przy tym nie tylko, że jjcl jest mniejsze od promienia zbieżności, ale także że jest mniejsze od 1. Rzeczywiście, jest

x* = Afo*—ji*^+t)+A_B x". i-o    1-0

Stąd, gdy n -*■ 00, otrzymamy żądaną równość, jeśli tylko jeszcze wykażemy, że A„ x" -*■ 0. W tym celu weźmy liczbę r spełniającą warunki

|x| < r < R, r # 1.

Wówczas |di| r' < L (dla / = 0, 1, 2,...) i

ix|"

\A„ x»| < L (l+    i- +    \ +    ... + -U    |xi" = -Ji-    (MV    _ -~-

\    r    r²    r" /    1—r    \ r }    1—r

To ostatnie wyrażenie dąży oczywiście do zera przy naszych założeniach.

§ 4. Własności szeregów zbieżnych

386. Prawo łączności. Pojęcie sumy szeregu nieskończonego tym różni się istotnie od pojęcia sumy skończonej liczby składników (rozpatrywanej w arytmetyce i algebrze), że zawiera w sobie przejście do granicy. Chociaż niektóre własności sum zwykłych przenoszą się także na sumy szeregów nieskończonych, najczęściej jednak dopiero wtedy, gdy spełnione są pewne warunki, które teraz będziemy badali. W innych wypadkach zwykłe własności sum, do których jesteśmy przyzwyczajeni, są w sposób rażący nie spełnione, tak że na ogół należy tu zachowywać ostrożność.

Rozpatrzmy szereg zbieżny

CO

(A)    ^a„ = ai+a₂+ ... +a«+ ...

a-l

Będziemy łączyli wyrazy tego szeregu w grupy w dowolny sposób nie zmieniając jednak przy tym ich kolejności:

a_x+ ... +a_Hi, a^+i-f ... +a_v ...,    a^+i-ł- ... +a_v

gdzie {n*} jest pewnym podciągiem ciągu liczb naturalnych.