0234

236

XI. Szeregi nieskończone o wyrazach stałych

Nierówność tę można napisać w postaci

1

(n + 1)*

J_ ' n*

Po prawej stronie mamy stosunek dwóch kolejnych wyrazów zbieżnego szeregu (H,) i stosując twierdzenie 3 stwierdzamy zbieżność szeregu (A).

Jeśli zaś, poczynając od pewnego miejsca, jest

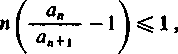
to otrzymamy stąd od razu

1

_> n _ »i + l a_n ^ n+l J_ n

i stosując twierdzenie 3 do szeregów (A) i (H) wnosimy, że szereg (A) jest rozbieżny.

Porównując kryteria d’Alemberta i Raabego, widzimy że drugie jest znacznie silniejsze od pierwszego. Jeśli istnieje granica ^<2> = lim‘2)„ i jest różna od jedności,

to ciąg 92„ = n --1^ ma granicę 92 równą + co, gdy <2) < 1, i równą — oo, gdy 9) > 1.

Jeżeli więc kryterium d’Alemberta daje odpowiedź na pytanie o zbieżności danego szeregu, to kryterium Raabego daje taką odpowiedź tym bardziej, co więcej: wszystkie takie przypadki są objęte przez dwie spośród możliwych wartości 92, a mianowicie wartości +oo i —co. Wszystkie pozostałe wartości 92, oprócz 92 = 1, rozstrzygające także kwestię zbieżności, odpowiadają więc przypadkom, gdy kryterium d’Alemberta na pewno kwestii tej nie rozstrzyga, bo 9) = 1.

Mimo to także tutaj w przypadku 92 = 1 nie mamy odpowiedzi na pytanie, czy szereg jest zbieżny. W podobnych przypadkach (bardzo rzadkich) trzeba się uciec do jeszcze subtelniejszych i bardziej skomplikowanych kryteriów [patrz np. dalej ustęp 371].

370. Przykłady

1) Zastosujemy kryterium Cauchy'ego do następujących szeregów. ⁰⁰ 1 1

(a) V-,    (?„ --,    0=0; szereg jest zbieżny.

“ (In «)"    ln n

(x > 0), S„ = —,    0 = 0; szereg jest zbieżny.

n

oc / \n

(c) y ( —) (x < 0, {a„}— ciąg o wyrazach dodatnich mający granicę a); Q„ = —. Jeżeli a = 0,

ir. V*/    ^a*

to 0 = + oo i szereg jest rozbieżny; jeżeli a = +oo, to 6 — 0 i szereg jest zbieżny, jeśli wreszcie