0238

240

XI. Szeregi nieskończone o wyrazach stałych

to mamy

°»tl ^ 1/fn + l

a. 1/ć.

na podstawie twierdzenia 3 szereg (A) jest też roz

Ponieważ szereg T' — był z założenia rozbieżny, więc

bieżny, c.b.d.o.

W postaci granicznej kryterium Kummera brzmi jak następuje: Załóżmy, że ciąg ^c^„ ma granicę (skończoną lub nieskończoną)

lim 9C„ = TC.

Wówczas gdy 9C>0, szereg jest zbieżny, a gdy 9C<0, szereg jest rozbieżny.

Pokażemy teraz jak można za pomocą kryterium Kummera otrzymać jako jego przypadki szczególne niektóre ważne kryteria zbieżności.

(a) Weźmy na przykład r„ = 1: warunek, by szereg ny. Mamy

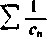
-1 .

byi rozbieżny, jest oczywiście spełnio-

1

tfn-H

2).

Jeśli 2). dąży do granicy 2), to 9C« dąży do granicy 9C =    — 1 (% — + co, jeżeli 2) = 0; °K = —1, jeżeli

<Z) = 4- oo). Jeżeli ^c2)> 1, to jest oczywiśiie 0C<0 i na mocy kryterium Kummera szereg jest rozbieżny. Jeśli <3< 1, to 9C>0 i szereg jest zbieżny. Doszliśmy więc znowu do kryterium d’Alemberta.

(b) Przyjmijmy dalej c, = n i zauważmy, że szereg -i-jest rozbieżny. Wyrażenie TT. będzie miało postać

TC, = n ——--(n-\-1) = 9?,—1 .

o*+i

Jeżeli 9?„ dąży do granicy 9?, to TC, dąży do 9?— 1 (9C = ± oc, gdy 9? = ± oo). Dla 92> 1, będzie 9C>0 i szereg zgodnie z kryterium Kummera jest zbieżny, jeśli zaś 9?< |, to 9C<0, a więc szereg jest rozbieżny. Otrzymaliśmy na nowo kryterium Raabego.

(c) Weźmy wreszcie r. = n In n (n > 2).

Taki wybór jest dopuszczalny, bo szereg Y —p—jest rozbieżny [367, 6]. Mamy w tym przypadku

^Ł— n In n

OC, = « ln u• ——--(n-|-1) In («-(-1).

dn+1

co można też przedstawić w postaci

*■ (-śr -■) -■]-kp -

gdzie przez 99„ oznaczyliśmy wyraz ogólny nowego ciągu

98.= lnit|*(-^--l) -lj =lnn (9e.-l).

Otrzymujemy stąd nowe kryterium