0252

254

XI. Szeregi nieskończone o wyrazach stałych

sprowadza się do zbieżności ciągu

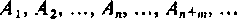
(1)

jego sum częściowych, naturalne jest zastosowanie do tego ciągu zasady zbieżności [39]. Nie zmniejszając ogólności można przyjąć, że z dwóch wspomnianych w niej wskaźników n i n' wskaźnik n' jest większy, n' > n, i przyjąć n' = n + m. gdzie m jest dowolną liczbą naturalną. Jeśli uwzględnimy to, że

^n+m    ^,,+1 "ł"2 4“ ...    ,

to zasadę zbieżności w zastosowaniu do szeregu możemy wysłowić jak następuje:

Na to, by szereg (A) był zbieżny potrzeba i wystarcza, by każdej liczbie e > 0 odpowiadaI taki numer N, że dian > N nierówność

(2)

l^n + l "bU„+2 “1“ ...    ■< £

jest spełniona dla każdego m = ł, 2, 3, ... (')•

Innymi słowy, suma dowolnej liczby wyrazów szeregu następujących po dostatecznie dalekim wyrazie powinna być dowolnie mała.

Jeżeli przy założeniu, że szereg jest zbieżny weźmiemy w tej nierówności m = I, to otrzymamy

|4«+il < £ (dla n > N),

a więc a„_+l -* 0 lub, co na to samo wychodzi, a_n -* 0, i otrzymujemy na nowo znany już warunek konieczny zbieżności szeregu [365, 5°]. Warunek ten żąda znacznie mniej niż warunek konieczny i dostateczny wymagający, by nie tylko każdy z osobna dostatecznie daleki wyraz szeregu, ale także i suma dowolnej liczby takich wyrazów była dowolnie mała! W związku z tym będzie bardzo pouczające powrócić do szeregu harmonicznego [365, 1)] i nierówności (1) wyprowadzonej dla jego wyrazów. Ogólny wyraz tego szeregu dąży wprawdzie do zera, ale nierówność (2) z tego ustępu nie jest spełniona dla żadnego n, jeżeli wziąć e = y i m = n, i wobec tego szereg harmoniczny jest rozbieżny.

Należy jednak powiedzieć, że sprawdzenie czy spełniony jest podany tutaj warunek konieczny i dostateczny zbieżności szeregu, jest zazwyczaj w konkretnych przypadkach bardzo uciążliwe. Dlatego jest ciekawe zbadanie klasy przypadków, w których zagadnienie zbieżności rozwiązuje się prostszymi środkami.

377. Zbieżność bezwzględna. Widzieliśmy w poprzednim paragrafie, że w przypadku szeregów o wyrazach dodatnich zbieżność stwierdza się najczęściej dość prosto, dzięki istnieniu wygodnych kryteriów zbieżności. Dlatego zaczniemy od tych przypadków, kiedy kwestia zbieżności danego szeregu sprowadza się do kwestii zbieżności szeregu dodatniego.

Jeżeli nie wszystkie wyrazy szeregu są dodatnie, ale począwszy od pewnego miejsca już takie są, to odrzucając dostateczną ilość wyrazów początkowych [364, 1°] sprowadzimy

(') Obaj autorzy zasady zbieżności — Bolzano i Cauchy wysłowili ją właśnie dla szeregów.