0240

242

XI. Szeregi nieskończone o wyrazach stałych

ność dla x>l. Jeśli zaś x 1, to weźmiemy stosunek

a. ^ (14-n) (y+/>) fl¹+i (¹+») (/?+»)

i korzystając ze związków 1

1- —+ ■

I+-Ł

1 +

14¹ •

" i+

2

przedstawimy go w postaci

o.,    _{= 1+} y-x—p+1 ₊ _ój_

o,+i    n    n¹

gdzie 6, jest ograniczone. Stosując kryterium Gaussa widzimy, że szereg F(x, /), y, jc) jest zbieżny, gdy y—x—(l>0, i rozbieżny, gdy y—^—f) < 0. Dalej powrócimy jeszcze do szeregu hipergeometryczr.ego przy ogólniejszych założeniach co do a, P, y i x.

2) Jako drugi przykład zastosowania kryterium Gaussa może służyć szereg

1 +

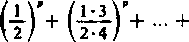
/ (2/>—1)!! \^P \    2/i U    /

+ ...

{p > 0),

który jest zbieżny dla p >2 i rozbieżny dla p < 2. Według wzoru Taylora mamy tu

Ot

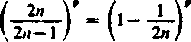
..Pi    .

2/1 1-2

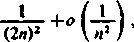
skąd

—p a

— = 1 + —--1——    (0„ - ograniczone)

o»+i    n zr

itd.

373. Kryterium całkowe Maclaurina-Cauchy’ego. Kryterium to różni się w swej formie od wszystkich poprzednich. Jest ono oparte na idei porównywania szeregu z całką i jest uogólnieniem tego chwytu, którym posługiwaliśmy się już dla stwierdzenia zbieżności lub rozbieżności szeregu w przykładach 4), 5), 6) ustępu 367.

Niech dany szereg ma postać

co    oo

(7)    £«„=£/(»),

l»²l    lt—1

gdzie /(«) jest wartością w punkcie x — n pewnej funkcji f(x) określonej dla x > 1 (^x); założymy, że funkcja ta jest ciągła dodatnia i monotonicznie malejąca.

1

Początkową wartością n może być zamiast 1 dowolna inna liczba naturalna zt₀, wówczas funkcję

2

f(x) także trzeba rozpatrywać dla x > n₀.