0224

226

XI. Szeregi nieskończone o wyrazach stałych

Niech szereg

00

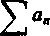
fil+<l2+ •••    •••

(A)

będzie dodatni, tzn. a_n > 0 (« = 1, 2, 3, ...). Wówczas jest oczywiście

•A»+l = A_n + a_H+_t ^ A_n,

tzn. ciąg {A_n} jest rosnący. Przypominając sobie twierdzenie o granicy ciągu monotonicz-nego [34] dochodzimy natychmiast do następującego twierdzenia podstawowego w teorii szeregów o wyrazach nieujemnych.

Szereg dodatni (A) ma zawsze sumę; suma ta jest skończona (a zatem szereg jest zbieżny), jeżeli sumy częściowe szeregu są ograniczone z góry, i nieskończona (a zatem szereg jest rozbieżny) w przeciwnym przypadku.

Wszystkie cechy zbieżności i rozbieżności szeregów dodatnich opierają się ostatecznie na tym prostym twierdzeniu. Jednak bezpośrednie zastosowanie tego twierdzenia w rzadkich tylko przypadkach pozwala wydać sąd o zbieżności szeregu. Podamy przykład tego rodzaju.

1) Rozpatrzmy szereg

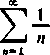
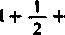
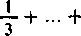
n

+ ... ,

znany pod nazwą szeregu harmonicznegoij). Zachodzi oczywista nierówność

(1)

1

n+1

+

I

n+2

+

+

2/i

> n

2/i

■>

Jeżeli po odrzuceniu dwóch pierwszych wyrazów, pozostałe wyrazy szeregu harmonicznego rozbijemy na grupy po 2,4, 8,..., 2*^-1,... wyrazów w każdej:

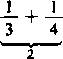
_L +J.+ -L + 1

5 ⁺ 6 ⁺ 7 ⁺ 8 ’

2¹

_L+    ₊ J_

9    ⁺ 16 ’

1

2‘-‘ + l

+

+ Y’

2*-i

to każda z tych sum z osobna będzie większa od -p Łatwo się o tym przekonać podstawiając do (1) kolejno n -= 2,4, 8, ..., 2"~‘,... Oznaczmy n-tą sumę częściową szeregu harmonicznego przez H_n; wówczas jest oczywiście

Hu >k•y .

Widzimy, że sumy częściowe nie mogą być ograniczone z góry-szereg ma sumę nieskończoną.

Wspomnimy już tutaj, że H_n rośnie ze wzrostem n bardzo wolno. Euler obliczył na przykład, że

H iooo = 7,48,    ...,    Jt, oooooo = 14,39,.

W przyszłości będziemy mieli okazję dokładniej scharakteryzować wzrost sum częściowych H„ [367, 10)]-(') Każdy jego wyraz, począwszy od drugiego, jest średnią harmoniczną dwóch wyrazów sąsied

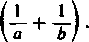
nich. Liczba c nazywa się średnią harmoniczną liczb a i b, jeśli — = -4

c 2