0344

346

XI. Szeregi nieskończone o wyrazach stałych

a zatem x 1, gdy N -*■ oo. Niech teraz N będzie na tyle duże, żeby: 1) spełniona była nierówność ó*+i < <e² i 2) odpowiednie x było tak bliskie 1, że zachodzi nierówność

%—O

Wówczas

n-0

co stanowi dowód tezy naszego twierdzenia.

Do rozpatrzonego przypadku szczególnego sprowadza się przypadek ogólny. Wyprowadźmy oznaczenie

v. = a, + 2a₂+ ... A-na, (n > 1), »_o = 0,

więc

i następnie

00

(7)    ^ a„ x'

H«0

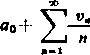
Rot

CD    00

-xf—o₀+(i—x)    y¹    —^v*‘    jc*⁺ⁱ .

Z_j    n    Z—i n (n+1)

Z założeń twierdzenia, tzn. z tego, że vjn -*■ 0, gdy n-+ <x>, łatwo otrzymać wniosek, że

(8)    lim (1—0.

*~i-o    n

II- t

Dla dowodu rozbijemy tę sumę na dwie

(l-*);£+<l-.x)f]

1    JW+l

i wybierzemy N w ten sposób, aby w drugiej sumie wszystkie współczynniki vjn były mniejsze od z góry danej liczby e >0. Wówczas cała druga suma będzie mniejsza od e dla każdego x. Jeśli chodzi o pierwszą sumę, która ma tylko skończoną liczbę składników, to możemy to samo osiągnąć kosztem przybliżenia x do 1.

Mamy więc wobec (7), (5) i (8)

(n+1)

lim V-2

i n(n-

^fl — A—a₀ •

Tu możemy już jednak zastosować udowodniony szczególny przypadek naszego twierdzenia, więc także

V—ił—

Z_J n (n+ 1)

n= 1

Z drugiej strony,

n

S

m-1

m (m+1)

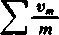
IM— 1

w    m

y v„ _ y _Pm__

Z—i m+1 Zl-i m    m

nt—1

Ponieważ pierwszy składnik dąży do zera, wynika stąd, że

lim £ a_m = A—a₀ ,

*-^co m-l

co kończy dowód twierdzenia.