0250

252

XI. Szeregi nieskończone o wyrazach stałych

wówczas dany szereg można napisać w postaci

Z

rt ■ 1

d.

Ai+«i

j zachowuje się on tak samo jak szereg

*

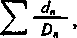
00

to znaczy tak samo jak szereg Z d_n (w przypadku rozbieżności można się powołać na wynik A bela

Ił— i

-Diniego).

Ostatni szereg jest zbieżny względnie rozbieżny zależnie od tego, czy ciąg u, jest ograniczony czy nie. 7) Niech będą dane dwa szeregi zbieżne

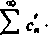
Mówimy, że drugi szereg jest wolniej zbieżny niż pierwszy, jeżeli reszta y' drugiego szeregu ma niższy rząd małości niż reszta y_m pierwszego szeregu, tzn.

lim-^s- =0.

*>/

Dla każdego szeregu zbieżnego Z ^c* ntożna utworzyć szereg zbieżny wolniej niż dany.

Ił—1

Wystarczy na przykład rozpatrzyć szereg

X    QC

<✓577-✓*)<■);

w tym przypadku y’_m = ]/y*.

Rozpatrzmy teraz dwa szeregi rozbieżne

oc    oo

S* i Z*'¹

N-l    ft-1

O drugim szeregu mówimy, że jest wolniej rozbieżny od pierwszego, jeżeli jego suma częściowa £>' jest wielkością nieskończenie dużą rzędu niższego niż suma częściowa D„ pierwszego, tzn. jeżeli

0.

Dla każdego szeregu rozbieżnego Z d, można utworzyć szereg rozbieżny wolniej niż dany.

»—1

Można w tym celu wziąć na przykład szereg

Z d:= Vdi+ z    •

«-l    ii-2

Tutaj D'„ = ]/D..

Analogiczne wnioski można też otrzymać za pomocą szeregów Abela i Diniego rozpatrywanych w 4) i 5).

(‘) Za y₀ przyjmujemy całą sumę Z