0256

258

XI. Szeregi nieskończone o wyrazach stałych

będący jak gdyby „nieskończonym wielomianem” ustawionym według potęg zmiennej x (a₀, a₁,a₂,... oznaczają tutaj stałe współczynniki). Już nieraz mieliśmy poprzednio do czynienia z takimi szeregami potęgowymi [patrz na przykład w poprzednim ustępie 1)

(a) - C«)].

Postaramy się teraz zdać sobie sprawę z tego, jaki kształt ma obszar zbieżności szeregu potęgowego, tzn. zbiór X = {x} tych wartości zmiennej, dla których szereg (4) jest zbieżny. Będzie to znowu ważny przykład zastosowania tego, co zostało wyżej wyłożone.

Lemat. Jeżeli szereg (4) jest zbieżny dla wartości x — x* różnej od zera, to jest on zbieżny bezwzględnie dla każdej wartości x spełniającej nierówność |x| < |jc*.|

Ze zbieżności szeregu

a₀+a_x x*+a₂ x*²+ ... +a_nx*ⁿ+ ...

>1*0

wynika, że jego wyraz ogólny dąży do zera [364, 5°], a zatem jest ograniczony (5) (n = 0,1,2, 3,...).

Weźmy teraz dowolne x, takie że |x| < |x*| i utwórzmy szereg

(6)

£Vx»| = |a₀l + Kx| + |<i₂x²|+ - +|a„x"|+ ..

Ponieważ [patrz (5)] jest

\a_n x"| = \a_n x*"|

wyrazy szeregu (6) są mniejsze od wyrazów zbieżnego szeregu geometrycznego o ilorazie |x/x*| < 1.

M-m-

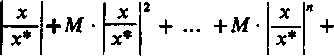
a więc na mocy twierdzenia 1 z ustępu 366 szereg (6) jest zbieżny. W takim razie, jak wiemy, szereg (4) jest zbieżny bezwzględnie, c.b.d.o.

Dla x = 0 jest oczywiście zbieżny każdy szereg (4). Istnieją jednak szeregi potęgowe,

które, oprócz tej jednej, nie są zbieżne dla żadnej innej wartości x. Przykładem takiego

wszędzie rozbieżnego szeregu potęgowego jest szereg £ n! x”, jak łatwo się przekonać

nm 1

za pomocą kryterium d’Alemberta. Podobne szeregi nie są dla nas ciekawe.

Załóżmy więc, że dla szeregu (4) w ogóle istnieją takie różne od zera wartości x = x*, dla których szereg jest zbieżny, i rozpatrzmy zbiór ich bezwzględnych wartości {|x*|}. Zbiór ten albo może się okazać ograniczony od góry, albo nie.

W tym ostatnim przypadku dla każdej wartości x znajdzie się na pewno takie x*, że |x| < |x*|, a zatem na mocy lematu szereg (4) jest dla tej wartości x zbieżny bezwzględnie. Szereg jest wszędzie zbieżny.