0280

282

XI. Szeregi nieskończone o wyrazach stałych

Przechodząc do przypadku ogólnego, napiszemy z, w postaci

_z _ (¹i-a)j'.+(¹ł-a)y.-i+ ... +(■¹.-a)yi j _ayi+y₂+ ... +y« u    n

Pierwszy składnik dąży tu do zera na mocy tego, co udowodniliśmy przed chwilą. Drugi składnik dąży

do ab, bo na mocy twierdzenia Cauchy’ego (1°)    -¹■ b.

n

5® Jeżeli x. -¹■ a, to także

x. =

i-¹.⁺ Q**+Q¹»+ ••• +

2”

•a O

Stosujemy twierdzenie II, przyjmując

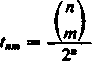
(n\    n^m

l<«¹,a -y- -¹■ 0 [32,9)j. Spełnienie warunków (b) i (c) wynika bezpośrednio z tego, że

M*0

6° Jeżeli x_n -¹■ a i z = const (z >0), to także

. ■•¹+fi) «¹■•<■(;) «•¹■+...+ Q-'»-0+¹)®

Jest to bezpośrednie uogólnienie poprzedniego twierdzenia i dowodzi się analogicznie. Można też ustawić współczynniki w dowolnej kolejności, a zatem jest też

//

X_n

*^,-x₀ + z^m~^,x_I+    — + ^1-1«

ó+z)®

392. Dalsze twierdzenia o mnożeniu szeregów. Jak wykazał F. Mertens wynik Cauchy’ego można, rozszerzyć na ogólniejszy przypadek.

Twierdzenie Mertensa. Jeżeli szeregi (A) i (B) są zbieżne, przy czym przynajmniej jeden z nich jest zbieżny bezwzględnie, to zachodzi równoii (13).

Dowód. Niech będzie zbieżny bezwzględnie na przykład szereg (A), tzn. zbieżny jest szereg (A®). Łącząc wyrazy it-tej przekątnej, przyjmiemy

c, — ai b.+ai ó«-i+ ...■ +a« bi,

C. = C1+C2+ ... +c_m ;

należy więc wykazać, że C_a -¹■ AB.

Przede wszystkim łatwo widać, że

(16)    C_m =    i,+«2    ... +a«-i ij+«« Bi.

1

Oczywiście nie jest istotne to, że numerację wyrazów ciągu zaczynamy od 0, a nie od 1.