0284

286

XI. Szeregi nieskończone o wyrazach stałych

co do wartości bezwzględnej mniejsze od e. Przechodząc do granicy przy m -» oo, otrzymujemy dla n > «₀ nierówność

n

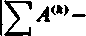
u_r

r-1

co wraz z (8) daje

A^m-U | < 2e,

fc—i

skąd wynika zbieżność szeregu iterowanego (3) właśnie do sumy U.

Uwaga. Niektóre wiersze macierzy (1) mogą zawierać tylko skończoną liczbę wyrazów. Wynik nasz rozciąga się łatwo na ten przypadek.

Jeśli przypomnimy sobie, że w 386 rozbijaliśmy wyrazy zwykłego szeregu tylko na skończone grupy, nie zmieniając przy tym porządku wyrazów, to zobaczymy, że twierdzenie 1 wypowiada daleko idące uogólnienie własności łączności i przemienności szeregów bezwzględnie zbieżnych.

Twierdzenie odwrotne zachodzi tylko przy wzmocnionych założeniach o szeregu ite-rowanym.

Twierdzenie 2. Niech będzie dany szereg iterowany (3). Jeżeli po zastąpieniu jego wyrazów ich wartościami bezwzględnymi otrzymuje się szereg zbieżny, to zbieżny jest nie tylko szereg (3), ale także zwykły szereg (6) składający się z tych samych co (3) wyrazów, ustawionych w dowolnym porządku, i jego suma jest równa sumie szeregu (3).

Dowód. Z założenia szereg iterowany

00 00

*»1 1-1

jest zbieżny, oznaczmy jego sumę przez A*. Dla dowolnych n i m jest

k~I 1-1

Weźmy teraz dowolną sumę częściową szeregu (6*)

U? = |Mil + |u₂|+ ... +|u_r| .

Dla dostatecznie dużych n i m wyrazy u_t,u₂, ...,«, będą zawarte w n pierwszych wierszach i m pierwszych kolumnach macierzy (1). Z (9) wynika więc, że

U* < A* ,

a zatem szereg (6*) jest zbieżny, tzn. szereg (6) jest zbieżny bezwzględnie.

Do zakończenia dowodu pozostaje już tylko zastosować twierdzenie 1.

Ponieważ wszystko, co zostało powiedziane o szeregu iterowanym (3) jest oczywiście słuszne także i dla szeregu (4), otrzymujemy jako wniosek z udowodnionych twierdzeń, ważne, często używane twierdzenie (').

W W literaturze niemieckiej nosi on nazwę grosser Umordnungssatz.