0266

268

XI. Szeregi nieskończone o wyrazach stałych

Rzeczywiście stosunek czynnika (n+l)-szego do czynnika n-tego wynosi

x+n+1    j | x+l

n

Ale [125, 4)]

analogicznie

1+

= i-*±L ₊j£^)L₊₀(4),

x+l    n    n^z    \n /

skąd

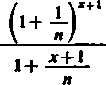
j ! (jr+1) x 2 n²

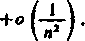
Z ostatniego wzoru widać, że dla (x+1) x>0 wspomniane wyrażenie staje się w końcu większe od 1, a dla (x+1) *<0 — jest mniejsze od jedności.

Aby stwierdzić ograniczoność czynników (14) powołamy się na to, że wyrażenie (14) ma skończoną granicę, gdy n -*■ oo, jak to będzie udowodnione dalej w ustępie 402,10). Wobec tego, zgodnie z kryterium Abela zbieżność szeregu (12) pociąga za sobą zbieżność szeregu (13). Jak zobaczymy, wspomniana granica jest zawsze różna od zera, dlatego podobny wniosek jest słuszny także dla odwrotności czynników (14). W takim razie na mocy tego samego twierdzenia zbieżność szeregu (13) pociąga za sobą zbieżność szeregu (12). Przez to jest wszystko udowodnione.

5) Podobny dualizm można ustalić dla zachowania się tak zwanego szeregu Lamberta

(15)

l-x*

i szeregu potęgowego [379]

(16)

a-l

o tych samych współczynnikach a, (wartości x — ± 1 oczywiście odrzucamy). Dokładniej: Jeżeli szereg

(A)    £

R-l

jest zbieżny, to szereg Lamberta (15) jest zbieżny dla wszystkich wartości x, w przeciwnym razie jest on zbieżny dokładnie dla tych samych wartości x, dla których jest zbieżny szereg potęgowy (16) (K. Knopp).

(a) Najpierw niech szereg (A) będzie rozbieżny, tak że promień zbieżności R szeregu (16) będzie mniejszy od jedności. Wykażemy, że dla jx| < 1 oba szeregi (15) i (16) zachowują się tak samo.