0328

330

XI. Szeregi nieskończone o wyrazach stałych

Rachunki, z dokładnością do 10 cyfr po przecinku, podajemy niżej.

y = 0,66666 66667 (-)

3-3-9

2

3-5-9²

2

3-7-9³

2

3.9.9*

2

3-11-9⁵

2

3-13-9®

2

3-15-9⁷

2

3-17-9*

= 0,02469 13580 ( + ) = 0,00164 60905 ( + ) = 0,00013 06421 ( + ) = 0,00001 12901 (-) = 0,00000 10264 (-) = 0,00000 00965 (-) = 0,00000 00093 (-) = 0,00000 00009 (+)

0,69314 71805

Uwzględniając wszystkie poprawki mamy

0,6931471802 < ln 2 < 0,6931471809

a zatem

ln 2 = 0,693147180 ...,

gdzie wszystkie napisane cyfry są poprawne.

Podstawiając teraz w (1) n = 4 otrzymujemy

ln 5 = 2 ln 2+ — (l+ ----— + ----L_ ₊ . \ .

9 \    3    81    5    81²    /

Korzystając z obliczonej już wartości ln 2, możemy z tego wzoru obliczyć ln 5, a następnie także ln 10 = = ln 2+ln 5. Potem można już z dowolną dokładnością obliczyć moduł

M =

1

ln 10

przejścia od logarytmów naturalnych do dziesiętnych; wynosi onM= 0,434294481... Mnożąc przez ten współczynnik, znajdziemy logarytmy dziesiętne log₁₀2 i log₁₀5

Przejdźmy teraz do logarytmów dziesiętnych w wzorze podstawowym (1):

Iog_I0(«+l)--!og₁₀ n

--L_ + J_---—

2n+l \    3    (2n+l)²    5    (2n+l)⁴

Podstawiając tutaj n = 80 =■- 2².10 i biorąc pod uwagę, że n+1 = 81 = 3*, otrzymamy

4 log_lo 3 —3 logio 2 — 1

2M_

161

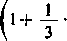
1

25921

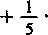
1

25921²

(2)