0274

276

XI. Szeregi nieskończone o wyrazach stałych

i dąży do granicy ln    Do tej samej granicy dążą też sumy A_ln-_x. Wreszcie na mocy uwagi z ustępu

389 sumą szeregu (6) jest ta sama liczba ln (2Vplq).

W szczególności dla szeregu (4) otrzymujemy sumę ln 2 (p = ą — 1) dla szeregu (3), tak samo jak w 1), -j- ln 2 (p = 1, g = 2). Analogicznie

¹⁺ł“ 2 ⁺ j‘ ⁺ł^_7⁺- “ł¹"^{2 (p = 2>} *⁼¹⁾

1-4-

±_JL_JL + ±_J---L _ _L _ J_ + i _ = o (p = 1, , = 4)

4 6 8 ^ 3 10 12 14 16 3    ^ ’ * ’

itp.

Zauważmy, że jeżeli liczebność kolejnych grup wyrazów dodatnich i ujemnych zmieniać jeszcze od grupy do grupy, to takie prawo zmiany można wybrać w ten sposób, aby dla przekształconego szeregu rzeczywiście otrzymać dowolną z góry daną sumę. Przekonanie się o tym pozostawiamy czytelnikowi.

389. Mnożenie szeregów. O dodawaniu (lub odejmowaniu) wyraz za wyrazem dwóch szeregów zbieżnych, jak też o mnożeniu wyraz za wyrazem szeregu zbieżnego przez stały czynnik mówiliśmy już w ustępie 364,3° i 4°. Teraz zajmiemy się mnożeniem szeregów. Niech będą dane dwa szeregi zbieżne

00

(A)    A —    = «i+«₂+ ... +a„+ ...

oraz

00

(B)    B =    = b_t+b₂+ ... + ó„+ ...

II—1

Naśladując regułę mnożenia sum skończonych, rozpatrzymy także i tutaj iloczyny parami a_t b_k wyrazów tych szeregów. Utworzą one nieskończoną macierz prostokątną

a i b,.	a2 b2	a3 bi	... atbt .
b2	a2 b2	03 b2	... atb2 .
<*i b3	a2 b3	a3b3	... a,b3 .
fli bk	a2 bk	a3 bk	... atbk .

Iloczyny te można na różne sposoby ustawiać w zwykły ciąg. Można na przykład porządkować te iloczyny po przekątnych lub po bokach kwadratów

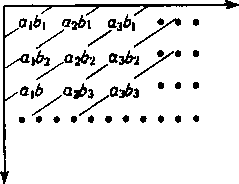
co prowadzi odpowiednio do ciągów: