0260

262

XI. Szeregi nieskończone o wyrazach stałych

Daje to bardzo proste i wygodne oszacowanie reszty rozpatrywanego szeregu, która sama też jest szeregiem naprzemiennym. Mianowicie, dla

72m ⁼ Cfrn+l ^2m+2"l"

jest oczywiście

0 < ?2m < c_2m +1,

zaś dla

?2m-l ^{= —} C_2m + C2_m + i+ ...

jest

72m-l < 0 i h/zm-ll < C_2m.

Tak więc we wszystkich wypadkach reszta szeregu naprzemiennego ma taki sam znak jak pierwszy wyraz tej reszty i jest mniejsza od niego co do wartości bezwzględnej.

Uwagę tę stosuje się często w rachunkach przybliżonych z użyciem szeregów [patrz 409]

382. Przykłady

1) Najprostszymi przykładami szeregów naprzemiennych są szeregi:

“ n    2    3    n

n» 1

Zbieżność obydwu szeregów wynika z udowodnionego twierdzenia.

Jednocześnie szeregi utworzone z wartości bezwzględnych ich wyrazów są rozbieżne. Dla szeregu (a) będzie to rozbieżny szereg harmoniczny, a dla (b) — szereg

1 +

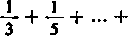
_1_

2n—1

+ ....

którego rozbieżność wynika łatwo stąd, że jego suma częściowa spełnia nierówność

*-»    4-1

Tak więc w szeregach (a) i (b) mamy pierwsze przykłady szeregów zbieżnych warunkowo. Zobaczymy niżej, że suma pierwszego szeregu jest równa In 2, a suma drugiego jest równa E ic [388,2); 405; 404], 2) Na mocy twierdzenia Leibniza są zbieżne szeregi

y (-D-¹

Z-1 «*

00

■-2

E

R-3

(-i)-¹ n In n ■ (ln ln n)‘

(s > 0).

Jeśli zastąpimy tu wszystkie wyrazy ich wartościami bezwzględnymi, to jak wiemy, dla s> 1 otrzymujemy szeregi zbieżne, a dla s < 1 szeregi rozbieżne. Tak więc dane szeregi są dla s>l zbieżne bezwzględnie, a dla s < 1 — zbieżne warunkowo.

Sxⁿ

—, który rozpatrywaliśmy w ustępach 370 i 378 może-

■*1

my teraz powiedzieć, że w końcu x = — 1 swego przedziału zbieżności jest on dla s < 1 jeszcze zbieżny lecz nie bezwzględnie.