0338

340

XI. Szeregi nieskończone o wyrazach stałych

Marków ustala warunki konieczne i dostateczne na to, by szereg £ A, był zbieżny do tej samej sumy A. Przekształcenie Markowa polega właśnie na tym zastąpieniu jednego szeregu iterowanego drugim:

CO    co

* ^A" k-l    1-1

Warunki dostateczne stosowalności przekształcenia Markowa podąje na przykład twierdzenie 3° z ustępu 393. Samo twierdzenie Markowa ma zresztą znacznie szerszy zasięg, nie zakłada bowiem nawet bezwzględnej zbieżności występujących szeregów.

Jako przykład zastosowania przekształcenia Markowa może służyć równość (13) z ustępu 39S. Cho-00

dzi o szereg    \/k², którego k-ty wyraz jest przedstawiony w postaci sumy, tym razem skończonej licz-

t-i

by składników

JT = <’+"?’+ ••• +<-,+'•» =

_ (*_,), r_i_i * i , _ i 11    (*—w

L 1*2- ... -(*+1)    2-3- ... -(*+2)    " (k-l)-k-... -(21—1)J    *^ł(k+l) ...(2*-l)‘

Następnie wykonuje się sumowanie według kolumn, co prowadzi do wspomnianej równości [patrz 393,4)]. Ciekawe będzie zauważyć, że gdybyśmy się posłużyli rozwinięciem

k²

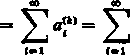
(fc-i)i

i(i+l) ...(»+*)’ przekształcenie Markowa, jak to już podkreślaliśmy w ustępie 393,4), nie dałoby nam nic nowego — po prostu wrócilibyśmy do wyjściowego szeregu.

Tworzenie macierzy (12) można by powiązać z iterowanym stosowaniem przekształcenia Kummera. Mówiliśmy już o tym w poprzednim ustępie [patrz (10)], ale tam powtarzaliśmy proces Kummera tylko skończoną liczbę razy, a tu powtarzamy go do nieskończoności. Należy przy tym tylko za każdym razem sprawdzać, czy „reszta” we wzorze (10) dąży do zera, tzn. czy jest

lim ^ *‘^w = 0.

■-“►li '

Aby się o tym przekonać na przykład w stosunku do (lOb), zauważmy, że występująca w reszcie

suma nie przekracza
	1 (pi)^1	CO
		lei
a więc cała reszta nie przekracza
	pl	00 V »

2»(2p-l)!l Z_i k²

lei

oczywiście dąży do zera, gdy p-*- oo. Przechodząc w wzorze (lOb) do granicy, otrzymujemy równość

yj_ _ 3IJ. + __L_. _L + _JL_.    +

Zj k² L 2    2-2*    3    3-2³    511

+

1

P-V

(2p-l)!l

]

_{= 3}Y-?___fr-m

Zj p-V (2p—1)11

P-ł

identyczną, jak łatwo zauważyć, z równością (13) z ustępu 395.