0312

314

XI. Szeregi nieskończone o wyrazach stałych

to w związku z 5° możemy stąd wnosić, że szereg

CO

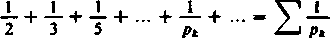
Ul

jest rozbieżny. Ważne to twierdzenie charakteryzuje ponadto w pewnym stopniu wzrastanie liczb pierwszych. Podkreślamy, że jest ono znacznie mocniejsze od twierdzenia o rozbieżności szeregu harmonicz-

nego Y —, bo chodzi tu tylko o część jego wyrazów.

, Jf 11*1

13) Analogicznie można udowodnić tożsamość (dla x> 1)

fM¹^)

gdzie znak plus lub minus po lewej stronie wybiera się w zależności od tego, czy (nieparzysta) liczba pierwsza ma kształt 4n— I, czy 4w+ I.

§ 7. Rozwinięcia funkcji elementarnych

403. Rozwinięcie funkcji w szereg potęgowy. Szereg Taylora. Rozpatrywaliśmy już w ustępie 379 szeregi potęgowe w postaci

CO

(1)    x" = a₀ + aj x + a₂ x² + ... +a„ x"+ ...

n»0

uporządkowane według potęg zmiennej x. Jeżeli wyłączymy szeregi wszędzie rozbieżne, to każdy taki szereg ma swój przedział zbieżności ( — R,R) o środku w punkcie x = 0, gdzie promień zbieżności R > 0, może jednak być też nieskończony. Końce tego przedziału dołącza się lub nie dołącza do obszaru zbieżności zależnie od konkretnego szeregu.

Rozpatruje się także szeregi potęgowe ogólniejszej postaci

CO

(2)    2>„(x-x_or = fl₀ + ai(*-x₀)+ •• +«»(*-*o)''+ -■

ii*>0

uporządkowane według potęg (x—x₀) zamiast x. Taki szereg nie różni się istotnie od szeregu postaci (1), sprowadza się bowiem do niego przez prostą zamianę zmiennych x - x₀ = y. Szereg (2) o ile nie jest wszędzie rozbieżny także ma swój przedział zbieżności od x₀ — R do x₀ + R; tym razem środek przedziału zbieżności jest w punkcie x₀. Końce jego, tak samo jak w przypadku szeregu (I), mogą do tego przedziału należeć lub nie.

W następnych paragrafach zbadamy szczegółowo własności szeregów potęgowych, które są pod wieloma względami podobne do wielomianów. Sumami częściowymi szeregów potęgowych są wielomiany, co czyni z szeregów potęgowych wygodne narzędzie do rachunków przybliżonych. W związku z tym wszystkim staje się bardzo ważne zagad-