0283

285

§ 5. Szeregi iterowane i podwójne

Suma tego szeregu będzie sumą szeregu iterowanego (3). Łatwo jest przystosować tę definicję także do szeregu (4).

Elementy macierzy (1) można na wiele sposobów uporządkować w zwykły ciąg

(5)    U], Wjj U3, u_n ... i utworzyć dla niego zwykły szereg

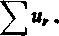
(6)

r-1

Mówiliśmy już o tym w związku z macierzami specjalnej postaci (7) w ustępie 389. Na odwrót, jeżeli mamy zwykły ciąg (5), to rozbijając jego wyrazy (bez uwzględnienia porządku) na nieskończenie wiele nieskończonych grup, można go przedstawić na wiele sposobów w postaci macierzy o dwóch wejściach (1) i z tej macierzy utworzyć szereg iterowany (3). Powstaje naturalne pytanie, jaki jest związek między szeregami (6) i (3) składającymi się z tych samych wyrazów.

Twierdzenie 1. Jeżeli szereg (6) jest zbieżny bezwzględnie i ma sumę U, to jakkolwiek ustawimy jego wyrazy w postaci macierzy (1), szereg iterowany (3) jest zbieżny i ma tę samą

sumę U.

Dowód. Szereg

CO

(6*)    y i«,i

r=l

jest z założenia zbieżny. Oznaczmy jego sumę przez U*. Jest więc przede wszystkim dla dowolnych n i k

\a?'\ < U* ,

i=*l

00 00 skąd wynika zbieżność szeregu £ |aj^ł)| [365], a zatem także i zbieżność szeregu £ ^af^y

i=i    i-i

dla każdego k [377].

Następnie, dla każdego e > 0 znajdzie się takie r₀, że

CO

(⁷)    l«,l < fi ,

r=r₀+l

a więc tym bardziej

00    ra

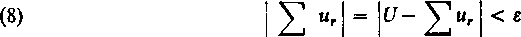
r=ro+l    r* 1

Wyrazy u_ltu₂, ... ,u_r (6) są zawarte w pierwszych n wierszach i pierwszych m kolumnach macierzy (1), jeżeli tylko n i m są dostatecznie duże, powiedzmy jeśli n > n₀, m > m₀. Wówczas dla takich n i m wyrażenie

n iw    rp

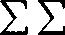
i=l    r-1

jest sumą grupy wyrazów u_r o wskaźnikach większych od r₀, a zatem na mocy (7) jest