035

2.34 Urćete argument p tak, aby platila rovnost:

a)    (cos |u + i sin |ti) (cos p + i sin p) = i

b)    (cos + i sin |n) (cos^? + isin<^) = — 1 cos + i sin _

cosy> + isin>£

„ cos łn + i sin

d) -⁵-. . ⁸    = -i

cosy> -f i sin p

2.35 Urćete v§cchna kornplexni Ćisla, ktera zc v§ech ćisel splńujicich podminku |z + 25| ^ 15 maji

a) nejyetśi absolutni hodnotu, b) nejmenśi argument.

2.36 Urćete graficky:
a) (2 +i) i	b) (2 - i) 2i
V 2 + i ^C) i
2.37 Urćete graficky:
a) (3 — 2i)(2 + i)
c) (1 + i)^4
2.38 V Gaussove rovine zvolte liboyolne ćisla z\, z2 a urćete graficky:
a) 2zi - I z2	, , Zi + Z-2 b) i
C) IZiZi	Z\ + Z-2 . ^d) - ^1

z i - z-i

2.39    Urćete obsah ćtyruhelniku, jehoż vrcholy jsou v Gaussove rovine ćisla z, z i, —z, —z i, kde z je dane komplexni ćislo.

2.40    V Gaussovć rovine je dan kosoćtverec O ABC tak, że bod A je obrazem ćisla 4 a uhel AOC ma velikost j7t. Urćete komplexni ćisla, jejichż obrazy jsou body B. C.

3 REŚENI ROVNIC V OBORU KOMPLEXNICH ĆISEL

Quidquid discis, tibi discis. Ćemukoli se ućiś, ućiś se pro sebe.

3.1 Kvadraticke roynice s realnymi koeficienty

Kvadratickou rovnici s realnymi koeficienty umirne dosud reśit jen tehdy, je-li jeji diskriminant nezaporny. Vime, ze ina dva ruzne realne kor eny, je-li kladny, a jeden dvojnasobny realny kor en, je-li roven nule. Pfipadem, że jeji diskriminant je zaporny, se budeme zabyvat nyni.

ReSme tedy rovnici

ax² + bx + c — 0, a,b,cE R, a ^ 0.

Obe jeji strany yynasobime nenulovym cislern a

(ax)² + abx + ac = 0

a levou stranu doplnime na druhou mocninu lincarniho dvojćlenu

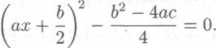
Po yynasobeni obou stran rovnice Ctyrmi dojdeme k rovnici

(2ax + b)² — (b² - 4ac) — 0,

ktera je ekvivalentnf s rovnici puvodni; ćislo D = b² — 4ac, jak vi-me, se nazyva diskriminant. Je-li diskriminant nezaporny, rovnici reśit umime; nebude vsak na śkodu, kdyź si postup, kterym se jeji kofeny ziskaji, pripomeneme.

69