0025

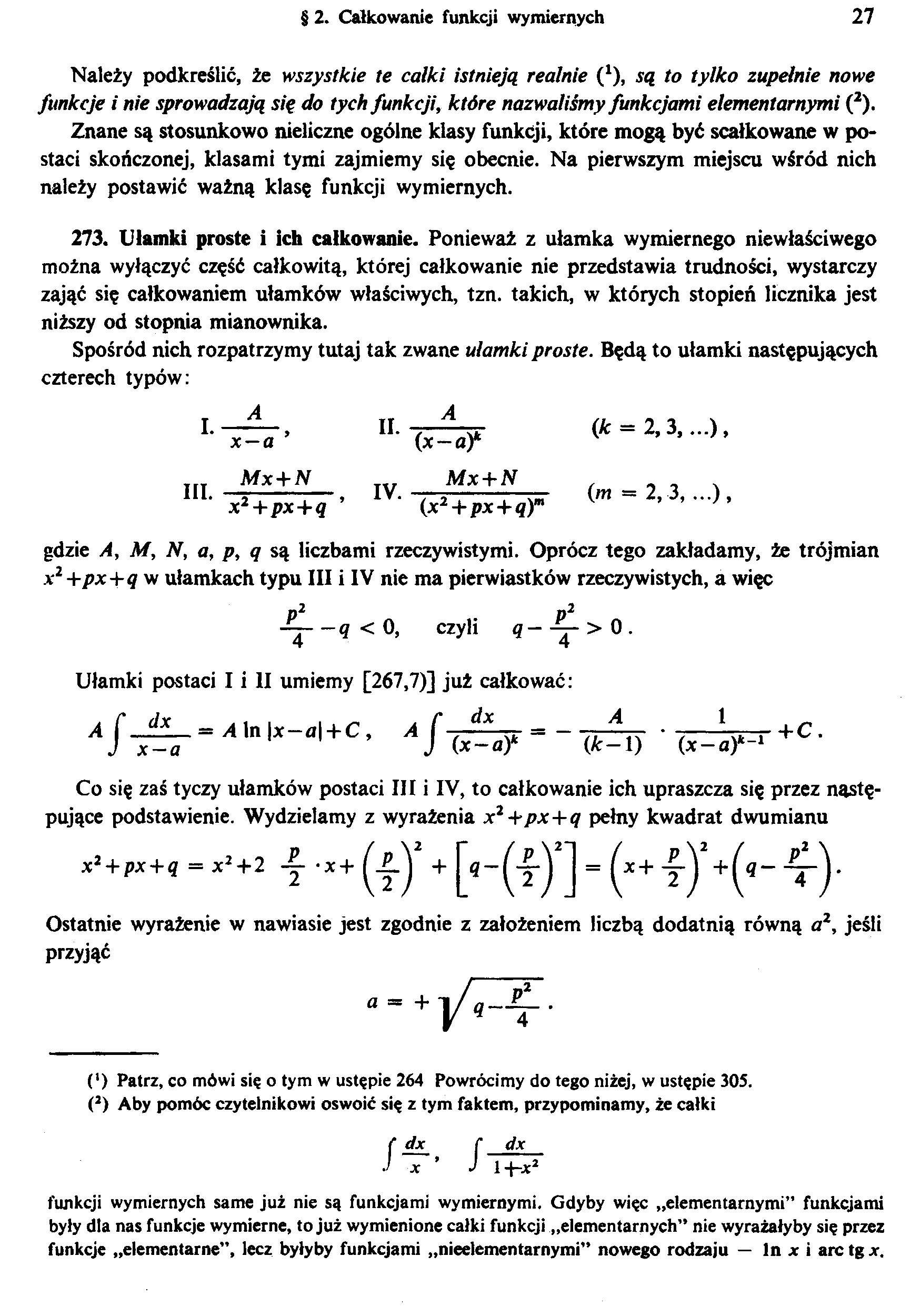
27

§ 2. Całkowanie funkcji wymiernych

Należy podkreślić, że wszystkie te całki istnieją realnie O, są to tylko zupełnie nowe funkcje i nie sprowadzają się do tych funkcji, które nazwaliśmy funkcjami elementarnymi (²).

Znane są stosunkowo nieliczne ogólne klasy funkcji, które mogą być scałkowane w postaci skończonej, klasami tymi zajmiemy się obecnie. Na pierwszym miejscu wśród nich należy postawić ważną klasę funkcji wymiernych.

273. Ułamki proste i ich całkowanie. Ponieważ z ułamka wymiernego niewłaściwego można wyłączyć część całkowitą, której całkowanie nie przedstawia trudności, wystarczy zająć się całkowaniem ułamków właściwych, tzn. takich, w których stopień licznika jest niższy od stopnia mianownika.

Spośród nich rozpatrzymy tutaj tak zwane ułamki proste. Będą to ułamki następujących czterech typów:

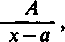
I.

II.

A

(x-af

III.

Mx+N x²+px+q ’

IV.

Mx + N (x² + px + q)^m

(k = 2,3,...), (m = 2,3, ...) ,

gdzie A, M, N, a, p, q są liczbami rzeczywistymi. Oprócz tego zakładamy, że trójmian x² +px+q w ułamkach typu III i IV nie ma pierwiastków rzeczywistych, a więc

^--q< o, czyli q-Ą^-> 0.

Ułamki postaci I i II umiemy [267,7)] już całkować:

A    A\n\x-a\ + C, A f .~^X~_k = --rr^-pr • ₇-^rT+^C-

J x-a    J (x-af    (k-1)    (x-a)*-^ł

Co się zaś tyczy ułamków postaci III i IV, to całkowanie ich upraszcza się przez następujące podstawienie. Wydzielamy z wyrażenia x²+px+q pełny kwadrat dwumianu

*•+*+« -*+^j i (ł)^!♦Hłj] - łH*- 4}

Ostatnie wyrażenie w nawiasie jest zgodnie z założeniem liczbą dodatnią równą a², jeśli przyjąć

a

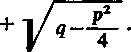
(') Patrz, co mówi się o tym w ustępie 264 Powrócimy do tego niżej, w ustępie 305.

(²) Aby pomóc czytelnikowi oswoić się z tym faktem, przypominamy, że całki

f ŚŁ. f dx

J x ’ J l+-x²

funkcji wymiernych same już nie są funkcjami wymiernymi. Gdyby więc „elementarnymi” funkcjami były dla nas funkcje wymierne, to już wymienione całki funkcji „elementarnych” nie wyrażałyby się przez funkcje „elementarne”, lecz byłyby funkcjami „nieelementarnymi” nowego rodzaju — ln x i arc tg x.