054

Dostavame tedy

MoAll |ApAl| _ Xi - 1 X? - Xj l^o^l 1^0^31    x\-x\ ⁺ X? - 1 ~

(*i - 1) (x? - 1) + (x? - x_x) (x? - x?)

(ar? - x?)(x? - 1)

—a;} + ar? + ar? — ar? — ari +1

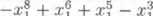
a protoźe x] — 1 a ar? — ari, mużeine pośledni ziomek upravit takto:

x? + ar? — x? - xi x? + x? - x? - Xi

Vztah, ktery jsme moli dokazat, tedy opravdu plati.

Priklad 4

V pravidelnem n-uhelniku A₀AiA₂ .. . /l_n-i oznaćme 5] soućet druhych mocnin velikosti vśech jeho stran a S₂ soućet druhych mocnin velikosti vsech jeho uhloprićek. Urćete S = Si + S₂.

Reśem

Soućet druhych mocnin velikosti stran a uhloprićek vychazejicich ze zvoleneho vrcholu Aq je

l^o^-il² + | j4o^4.2 |² + |^4o^4.3 I” + • ■ • + \AoA_n-i |²,

a protoże vrcholu je celkem n a każda strana i uhloprićka by była timto zpiisobem poćitana dvakrat, plati pro hledany soućet S:

S — 2    |² + \A₀A₂\'² + ... + |v4odln-i|² j

K urćeni tohoto soućtu umistime pravidelny n-uhelnik AqA\ ... A„-1 v Gaussovć rovine tak, aby jeho vrcholy Ak były obrazy ćisel

x k =

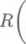
2Ara . . 2A:it cos--h i sin-

n

k = 0,1,2,.. .,n — 1,

ktera jsou kofeny binomicke rovnice xⁿ — R⁷¹ = 0; je zrejme, źe R je polomer krużnice danemu n-uhelniku opsane.

Każdy sćitanec |AoiU|² soućtu S vyjadfiine ve tvaru

\A₀A_k\² - |z* - xq\² = ja?it - R\² =

= (x_k - R)(xk - R) = (x_k - R) (2fc - R) a s ohledem na to, ze plati

Xl — X_n—\, X'2    X_n—21 • • • j %n—2    *^2?    1    X\^

dostaneme

S = ^ [(^1 - R)(x_n-1 - R) + (x₂ - R)(x_n-2 -fi) +

+ ••■+■ (Zn-l ~ R)(X 1 ~ ^)] •

Vzhledem k tomu, źe plati

XiXn—1    X'2Xn—2 — • • * — Xn—1X1 — R ,

inużeme dale upravit

S = — [2(n — l)i?² — (ii R + x_n—\R + x₂ fi + x_n—₂R +

+ ... + x_n—\R + xji?)] =

= ^ [2(n - l)i?² -2R(xi + x₂ + • • • + £n-i)].

Protoże vsak pro kofeny binomicke rovnice xⁿ — a — 0 plati Xo +    + X2 + . • • + 3I_n—1 = 0,

znamena to v naśem pripade, kdy je xq = R, źe x\ + x₂ + ... + x_n-1 = —R.

Dosazenim tohoto vysledku do souctu S dostaneme

S = — [2(n — l)i?² — 2R{x\ + x₂ + ... +    —

- 2 [2(n - 1 )R? - 2fi(-fi)] = n?R².

107