058

Tim je odvozena kosinova veta, nebot’ z pośledni rovnosti cyklickou zamenou dost.avame take

b² — <? + o² - 2ca cos 3, c² = a² + b² - 2abcos~f.

K odvozeni v£ty sinove doplnime trojuhelnik ABC na obr. 4.6 na rov-nobeźnik ABCD tak, że bod D je obrazem komplexniho ćisla

o [cos (k — 3) + i sin (ic - /?)] = a(- cos 3 + i sin/?).

Z geometrickeho vyznainu sćitani komplexnich ćisel vime, że plati

c + a(— cos 3 + i sin3) = 6 (cos a + i sin a),

a porovnanim imaginarnich ćasti dostaneme, że plati

a sin 3 — b sin a.

Tim je odvozena sinova v6ta. nebot’ z teto rovnosti cyklickou zamenou dostavame take

b sin 7 = c sin 3, c sin a = a sin 7.

Pro uplnost. poznamenejme, że porovnanim realnych casti komplexnich Cisel v rovnosti

c + a (— cos 3 + i sin 3) = b (cos a + i sin a)

a naslednou cyklickou zamenou dostavame tzv. vetu o prumetech:

c = a cos 3 + b cos a a = b cos 7 + c cos 3 b = c cos a + a cos 7

A

jfłeśer

Urćete soućet:

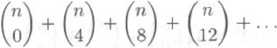
Uvedomte si nejprve, że jde o soućet konećneho poćtu nenulovych

⁽n\

sćitancu, nebot’ pro k > n je

= 0. Podle binomicke vety je

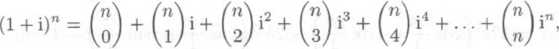
(1 — i)ⁿ =

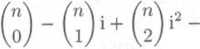
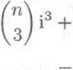
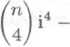
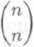
a sećtenun techto dvou rovnosti dostaneme

(1 + i)ⁿ + (1 - i)ⁿ = 2

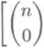
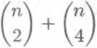
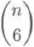
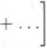
Uvedomime-li si dale, że

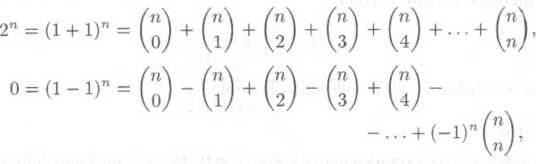
dostaneme sećtenun techto dvou rovnosti

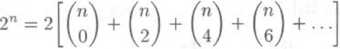
115