1077

badanych jednostek zbiorowości, podczas gdy miary pozycyjne wskazują określ ną pozycję jednostek (np. środkową lub dominującą).

Schemat 4.1. Klasyfikacja miar średnich

MIARY PRZECIĘTNE

KLASYCZNE    _    POZYCYJNE

• średnia arytmetyczna x    • dominanta D_tt

•    średnia harmoniczna x_h    • mediana Me

•    średnia geometryczna 7₀-

Źródło: opracowanie własne.

4.3.1. KLASYCZNE MIARY ŚREDNIE

Średnia arytmetyczna

Średnia arytmetyczna wyraża przeciętny poziom badanej cechy (zmiennej w populacji np. przeciętna miesięczna sprzedaż, średnia ocena na świadectwie szkolnym itp. Interpretacja średniej i metoda jej wyznaczania jest zawsze taka sama, jednak techniczny sposób obliczenia średniej zależy od typu szeregu statystycznego, z którym mamy do czynienia (czyli od postaci materiału statystycznego, z którego korzysta badacz). Średnia jest sumą wartości cechy podzieloną przez liczbę jednostek zbiorowości.

Średnią arytmetyczną będziemy oznaczać symbolem x.

Najprostszy sposób jej wyznaczenia odnosi się do przypadku szeregu szczegółowego, w którym mamy pojedyncze wartości cechy dla każdej jednostki statystycznej i średnią liczymy następująco:

x

^Xl ⁺*2 +••• + %

N

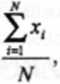
(4.4)

gdzie:

N - liczebność całej zbiorowości statystycznej,

x, =x_lf x₂, x₃ x_N - kolejne wartości cechy mierzalnej poszczególnych jed nostek statystycznych.

Średnia arytmetyczna określona wzorem (4.4) nosi nazwę średniej arytmetycz nej prostej (nieważonej) i ma ona zastosowanie jedynie w przypadku, kiedy dyspo nujemy szeregiem szczegółowym lub danymi indywidualnymi.

Przykład 4.5

W dziale marketingu firmy X jest zatrudnionych pięciu pracowników, których staż pra-ęy (w latach) na dzień 30 czerwca 2004 roku wynosił odpowiednio: 3: 3.5: 4; 4.5; 5. Jaki był ^Jedni staż pracy pracowników tego działu na dzień 30 czerwca 2004 roku?

Rozwiązanie

Badana przez nas cecha to staż pracy pracownika. Oznaczamy więc kolejno: x_{ = 3, _t, = 3.5, x₃ = 4, x₄ = 4,5 x₅ - 5. Liczba objętych badaniem jednostek wynosi 5 (W = 5).

Przystępujemy do obliczania średniego stażu pracy:

5

__x₁+s_ł+-»:,+x₄+s_s _    _ 3 + 3,5 + 4 + 4,5 + 5 _ ^ _bb

*    N    N    5

Średni staż pracy pracowników działu marketingu firmy X na dzień 30 czerwca 2004 r. wynosił 4 lata.

W sytuacjach, kiedy mamy do czynienia z liczniejszymi zbiorowościami, tzn. jeżeli poszczególne wartości cechy występują więcej niż jeden raz, to przy wyliczaniu ich średniej wartości należy każdą z nich uwzględnić tyle razy, ile występuje. Taką średnią nazywamy średnią ary tmetyczną ważoną.

Średnią arytmetyczną ważoną wyznaczamy sumując poszczególne wartości cechy pomnożone przez odpowiadające im wagi (liczebności) i dzieląc tak otrzymaną wartość przez liczbę obserwacji. Z tego rodzaju sytuacją mamy do czynienia w szeregach rozdzielczych punktowych i przedziałowych. Wzór na obliczenie średniej arytmetycznej dla szeregu rozdzielczego punktowego ma następującą postać:

•n₂ +...+x_kn_k N

M

N

(4.5)

gdzie:

k - liczba klas szeregu statystycznego,

i = 1, 2,.... k- numery kolejnych klas szeregu statystycznego,

n, - liczebność klasy szeregu rozdzielczego o numerze i,

x_t - wartość cechy mierzalnej w- klasie szeregu rozdzielczego o numerze i.

Przykład 4.6.

W klasie III b średnia ocena z matematyki na koniec semestru zimowego wynosiła 3,5, natomiast uczniowie III a uzyskali w badanym okresie następujące oceny z matematyki: 1:1; 2; 2; 2; 2; 3; 3; 3; 3; 3:3: 3; 3; 3: 3; 3,5; 3,5; 3,5; 3,5; 4:4; 4; 4; 4.5: 5; 5; 6.

Jaka była średnia ocena z matematyki w III a? Która klasa przeciętnie rzecz biorąc miała lepsze oceny z matematyki w semestrze zimowym?

93