1131

Wielkości w kolumnie trzeciej są indeksami łańcuchowymi wyliczonymi zgodnie z for-

mulą 7.5. Wszystkie wskazują na to, iż liczba absolwentów szkół wyższych w kolejnych latach analizowanego okresu wzrastała, ponieważ przyjmują wartości większe od jedności. Najszybszy był wzrost w roku 1996, na co wskazuje największa wartość indeksu w tym roku, najniższy wzrost zanotowano w roku 2002 (indeks najmniejszy). W kolumnie piątej tabl. 7.6. znajdziemy indeksy łańcuchowe przeliczone na procenty i nazwane .Rok poprzedni=100*. zgodnie z zestawieniem pokazanym w tabl. 7.5. interpretacja przykładowa liczb z tej kolumny jest następująca:

•    w roku 1996 liczba absolwentów szkół wyższych stanowiła 130,2% liczby absolwentów z roku 1995,

•    w roku 2002 liczba absolwentów stanowiła 112.5% liczby absolwentów z roku 2001.

Analogiczne obliczenia przeprowadzono dla wersji jednopodstawowej indeksu, którego

wartości znajdują się w kolumnie czwartej tabl. 7.6. Jeśli indeksy łańcuchowe wskazywały na wzrost zjawiska we wszystkich latach analizowanego okresu to indeks, którego podstawą jest pierwszy rok badanego przedziału czasowego, będzie przyjmował wartości znacznie przekraczające jedność w końcu tego okresu. Wartość 3,844 w ostatnim wierszu tej kolumny może być interpretowana tak: w roku 2002 liczba absolwentów szkół wyższych jest blisko czterokrotnie większa w porównaniu z liczbą studentów, którzy ukończyli szkoły wyższe w roku 1995. Po przeliczeniu indeksu jednopodstawowego na procenty (kolumna szósta) wskaźnik dla roku 2002 możemy zinterpretować następująco: liczba absolwentów szkół wyższych w roku 2002 stanowi 384,4% liczby absolwentów z roku 1995 (odnotowano wzrost wynoszący 284,4%).

Jak wcześniej zauważono, najczęściej wykorzystywaną miarą dynamiki są przyrosty względne. Zarówno w opracowaniach naukowych, jak też w prasie fachowej czy codziennej podawane są informacje o tym, o ile procent zmieniło się pewne zjawisko. Indeksy dają się łatwo przeliczyć na tempa zmian, ponieważ obie miary łączy proste przekształcenie algebraiczne:

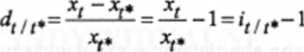
(7.7)

Analogiczną relację zapisać możemy, gdy obie kategorie: przyrost względny i indeks wyrażone są w procentach:

(7.8)

Zatem, jeśli korzystamy z publikowanych indeksów w wyrażeniu procentowym, wystarczy od tego indeksu odjąć 100% i otrzymujemy tempo zmian w %.

Tablica 7.7. Liczba absolwentów szkół dla dorosłych i jej dynamika

w latach 1995-2002

Rok	Absolwenci szkół dla dorosłych w tys.		Vi-r 1°0	^dVt-l	<W'00
1	2	3	4	5	6
1995	61.4		•	•	•
1996	67,8	1,104	110,4	0,104	10,4
1997	74.9	1,105	110,5	0,105	10,5
1998	82,4	1,100	110,0	0,100	10,0
1999	89,6	1.087	108,7	0,087	8.7
2000	98,0	1.094	109,4	0.094	9.4
2001	99,5	1,015	101,5	0,015	1.5
2002	99,2	0,997	99,7	-0,003	-0.3

Źródło: obliczenia własne na podstawie danych z Rocznika Statystycznego Rzeczpospolitej Polskiej 2003, Rok LXItl, GUS. Warszawa 2003, s. XUV-XLV, tabl. I, lp.21.

Przykład 7.6.

W tablicy 7.7 zestawione są absolutne wielkości liczby absolwentów szkól dla dorosłych oraz wyznaczone dla tej kategorii indeksy łańcuchowe i przyrosty względne łańcuchowe. Dla lat 1996-2001 obserwujemy wzrost liczby absolwentów, indeksy są większe od jedności (lub większe od 100% w ujęciu procentowym), a przyrosty względne dodatnie. W roku 2002 nastąpił spadek liczby absolwentów w stosunku do roku 2001. zatem indeks przyjmuje wartość mniejszą od jedności (od 100%), a przyrost względny jest ujemny. Spadek notowany w roku 2002 jest niewielki, bo stanowi 0,3% wielkości z roku 2001. Znaczne były natomiast przyrosty względne tej kategorii w latach 1996-2000, które kształtowały się na poziomie ok. 10% z roku na rok.

Mając do dyspozycji różne miary dynamiki wybierzemy taką ich wersję, która pozwoliłaby odpowiedzieć na pytania, które nas nurtują.

Przykład 7.7.

Rozważmy zestawienie nakładu książek i broszur wydanych w ostatnich latach (por. tabl. 7.8).

Tablica 7.8 Nakład książek i broszur i jeco dynamika w latach 1995-2002

Rok	Nakład w min sztuk	^At’t-1	dw_, • 100	»Vr_f • 100	^At/1995	^dt'199S ' ^100	Vf995 ^1 00
1	2	3	4	5	6	7	8
1995	116.0		•		0	0	100,0
1996	80.3	-35.7	-30,8	69,2	-35,7	-30.8	69,2
1997	93,7	13.4	16,7	116,7	-22,3	-19,2	80,8
1998	85,0	-8.7	-9,3	90,7	-31,0	-26,7	73.3
1999	78,1	-6,9	-8.1	91.9	-37,9	-32,7	67.3
2000	103,0	24,9	31.9	131,9	-13.0	-11.2	88.8
2001	74,4	-28.6	-27,8	72,2	-41.6	-35,9	64,1
2002	67,6	-6.8	-9,1	90.9	-48.4	-41.7	58.3

Źródło: obliczenia własne na podstawie danych z Rocznika Statystycznego Rzeczpospolitej Polskiej 2003, Rok LX///, GUS, Warszawa 2003, s XLVI-XLVII, tabl. I. Ip.9.

201