img279

wielkości, ale ponadto jej kolumny (wiersze) są niemal współliniowe, a zatem macierz C jest niemal osobliwa. Wtedy otrzymanie wystarczająco dokładnych¹ rozwiązań układu równań normalnych wymaga zastosowania odpowiednich procedur o dużej precyzji obliczeń. Pewnym praktycznym zabiegiem poprawiającym dokładność numeryczną obliczeń jest sprowadzanie poszczególnych zmiennych do postaci półlogarytmicznej: podzielenie każdej z nich przez taką potęgę 10, aby jej wartości miały jedną cyfrę przed przecinkiem, tzn. należały do przedziału <1, 10). Wtedy współczynniki regresji zwiększą się w tym samym stosunku, a wszelkie testy statystyczne nie ulegną zmianie.

Analizę regresji krzywoliniowej według modelu wielomianowego można znacznie ułatwić, jak również zmniejszyć pracochłonność obliczeń, gdy zmienna objaśniająca X jest kontrolowana i możemy dobrać jej wartości tak, aby tworzyły ciąg arytmetyczny, tzn.

(13.5)

x,+1 = Xj + n=+ ih

Wówczas transformację modelu regresji wielomianowej (13.3) na model regresji wielokrotnej możemy przeprowadzić tak, aby poszczególne zmienne w modelu wielokrotnym były parami nieskorelowane (ortogonalne). Daje to w efekcie macierz układu równań normalnych C postaci diagonalnej. Wtedy cały układ równań normalnych rozpada się na p niezależnych równań liniowych z jedną niewiadomą każde, rozwiązuje się go więc natychmiast. Również obliczenie macierzy odwrotnej do C jest proste, mianowicie macierz C ^_1 ma na przekątnej odwrotności elementów leżących na przekątnej macierzy C, a poza tym zera, jest więc diagonalna. Dlatego też analiza istotności poszczególnych zmiennych w regresji wielokrotnej jest prosta — każda zmienna może być testowana niezależnie od innych, a kolejność testowania nie ma znaczenia.

Transformacji, o której mówimy (ma ona nazwę tzn. ksi prim), możemy dokonać posługując się układem wielomianów ortogonalnych. Wartości wielomianów ortogonalnych w punktach x, spełniających warunek (13.5) tworzą właśnie układ nieskorclowanych danych².

Wielomiany te £,<*) do czwartego stopnia łącznie dane są wzorami:

ę, (.x) = k(x)\_l

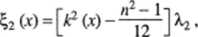
się spełnienia warunku (13.5), nic będziemy jej jednak tu omawiać.

279

1

   w sensie numerycznym

2

   Istnieje również znacznie bardziej złożona metoda ogólna wielomianów ortogonalnych, w której nie żąda