CCI20090825010

PARAMETRY OPISUJĄCE STAN DYNAMICZNY

MIESZANINY

371

Tak więc dla n,-» co mieszaniny ciągłej wariancja randomowa równa

Wzoru (7-36) nie możemy stosować do mieszanin rzeczywistych. Dla takich mieszanin wariancję a² należy obliczać z odpowiednich wzorów empirycznych.

Dla rzeczywistych mieszanin dwuskładnikowych charakteryzujących się rozkładem wymiarów ziarn obu składników, Stange [45] podał wzór do obliczenia wariancji stanu randomowego

„z ₌    [(i-_Xa)m_A(l +/_a²)+*a '»„(! +/.*)]

(7-37)

gdzie: m — masa próbki, »i_A, m, — średnie masy ziarna składników A oraz B, .v_A — udział masowy

składnika A w mieszaninie, /*, /„ — współczynniki zmienności mas będące stosunkiem odchylenia standardowego masy ziarna do jej wai

Dla mieszaniny rzeczywistej składającej się z frakcji sitowych tego samego materiału Buslik [8] podał wzór

Xą(1-Xą)»'za _[ *a(»V

(7-38)

gdzie: m, — średnia masa ziarna mieszaniny obliczana addylywnie z udziałów masowych frakcji,

7.4.2. Stopień zmieszania

Badanie kinetyki procesu mieszania wymaga kontroli stanów pośrednich mieszaniny (pomiędzy stanem całkowitego rozmieszania oraz stanem zmieszania).

Informuje o tym wariancja próby a², jednak wielkość ta jest funkcją udziału składnika kluczowego, a więc nie stanowi jednoznacznej (ogólnej) miary stanu mieszaniny. Najbardziej przydatny do takiej oceny jest tzw. stopień zmieszania.

Stopień zmieszania określa najogólniej oddalenie układu od stanu równowagi mieszaniny idealnej, jakim jest stan randomowy.

Jeżeli jako miarę tego oddalenia przyjmiemy różnicę wariancji o²—o², wówczas odnosząc tę różnicę do jej wartości maksymalnej {o²— o))t(a^ — a²) uzyskamy zredukowaną miarę stanu zmieszania, czyli stopień zmieszania zmieniający się od 1 do 0. Najczęściej jako stopień zmieszania przyjmuje się wielkość 1 -(o² - o²)l(er₀² - o²), która zmienia się od zera dla stanu całkowitego rozmieszania, do jedności dla stanu zmieszania randomowego

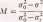
(7-39)

Jeżeli jako miarę oddalenia stanu mieszaniny od stanu randomowego przyjmiemy różnicę ó—<r_r, wówczas definicja stopnia zmieszania przyjmie postać

(7-40)