0136

137

§ 4. Ciągłość (i punkty nieciągłości) funkcji

Tak więc dla dodatnich x postaci ml2" mamy:

(15)    f(cx)=cos 9x.

Ponieważ dowolną liczbę dodatnią x można przedstawić jako granicę x-ów tej postaci, to przez przejście do granicy (i wykorzystanie ciągłości funkcji f(x) i cos x) stwierdzamy słuszność wzoru (15) dla wszystkich x>0. Dla jc=0 wzór jest słuszny na podstawie (10), a dla x<0 na mocy (11). Jeżeli w (15) zastąpimy x przez xlc i przyjmiemy 0/c=a, to otrzymamy w końcu:

f(x) =cos ax.

W przypadku (fł) mamy: f(c)> 1; w takim razie znajdziemy takie 0, że

/(c)=cosh0.

Powtarzając dosłownie wszystkie poprzednie rozważania i korzystając ze wzorów dla kosinusa hiper-bolicznego zgodnych co do postaci z odpowiednimi wzorami dla kosinusa trygonometrycznego, znajdujemy w rozważanym przypadku, że

/(x)=cosh«x (a>0).

Przy o=0 otrzymalibyśmy z obu wzorów, że /(¹)== 1.

Równania funkcyjne (A), (B), (C), (D) i (E) rozpatrywał po raz pierwszy Cauchy, który podał ich rozwiązania w funkcjach ciągłych.

77. Wykorzystanie ciągłości funkcji dla obliczania granic. Ciągłość funkcji może być w różny sposób wykorzystana przy obliczaniu granic(¹). Przykładom takim poświęcamy ten ustęp.

1) Dla dowolnego rzeczywistego x mamy

lim

n -* + oo

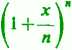
X

=e .

Rzeczywiście, rozpatrywane wyrażenie (przy ¹#0) można przedstawić w postaci

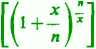
Ponieważ xjn-¹0, więc ciąg w nawiasie kwadratowym dąży do e [54 (13)] i na mocy ciągłości funkcji potęgowej (tu x=const) całe wyrażenie dąży do e^x.

2) Znaleźć granicę

lim [-^U+a, (x+a₂)...{x+a_k)-x]    (oo-oo).

X-¹ + oo

gdzie a_t, a₂,.... a¹ są danymi stałymi liczbami. Korzystając z tożsamości

/-z^k

^{y Z}~/-'+/-¹z+...+z^k-''

gdzie podstawiamy

y=^/(x+ai)...(x+a_k) oraz z=x,

1

Faktycznie, czyniliśmy tak już niekiedy przedtem; np. w przykładzie 3) [56] ustaliliśmy po

m —

drodze ciągłość Vx przy x= 1 i korzystaliśmy z niej; w przykładzie 5) b) podobnie postąpiliśmy z cos x dla x=0.