Egzam z Żelbetu semestr2 str 0003 bmp

Prof. dr hab. Inż. WŁODZIMIERZ STAROSOLSKI

Politechnika Śląska

0 modelowaniu belek w stropach ptytowo-żebrowych

Ogromną zaletą obliczeń komputerowych jest możliwość odwzorowania w jednym modelu obliczeniowym całego stropu, włącznie z podpierającymi go belkami, słupami i ścianami, w pełni ze sobą współpracującymi. Jednak odwzorowanie belki w modelu obliczeniowym może być bardzo różne (szerzej w (4], a także w [1]). Dalej przedstawiono, w celu porównania, wpływ sposobu modelowania belki będącej częścią modelu stropu na wyniki obliczeń w przypadku podstawowych sytuacji konstrukcyjnych oraz kilka zaleceń praktycznych w tym względzie.

Strop jednoprzęstowy poprzecznie nieskończony

W stropie {rys. 1) przyjęto, że ściany podpierające stanowią podpory liniowe niepodatne, a obciążenie całkowite wynosi 10 kN/m². W kierunku poprzecznym strop nosi znamiona stropu nieskończonego.

y HikNnf

*»»*i***t«**t*'

■' ir

U ' -

t—u----r ^-

ii ii 11 u II ::

11 I

i . J L -

___11__

_ JL_ J

Rys. 1. Rzut analizowanego stropu płytowo-żebrowego

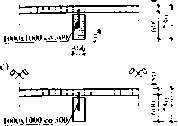
Analizowano 7 modeli obliczeniowych żeber stropu (rys. 2):

a) strop modelowany wyłącznie elementami powłokowymi (rys. 2a),

b) płytę stropową oddzieloną od belki na krawędzi poziomego styku pod powierzchnią płyty i połączoną sztywnymi elementami zaczepionymi w osi płyty (modelowanej elementami powłokowymi) i w osi odciętej belki (także modelowanej elementami powłokowymi); przyjęto, że każdy taki sztywny element ma wymiar poprzeczny 1,0 x 1,0 m (rys. 2b),

c) płytę stropową oddzieloną od belki na krawędzi poziomego styku pod powierzchnią płyty i połączoną sztywnymi elementami zaczepionymi w osi płyty i w osi odciętej belki, jak w punkcie b), jednak zamiast belki w postaci powłoki, na końcu sztywnych prętów umieszczono pręt o wymiarach 0,6 x 0,3 m: przyjęto jak poprzednio, że każdy taki sztywny element ma wymiar poprzeczny 1,0 x 1,0 m (rys. 2c).

d) model, w którym wzdłuż osi żebra wprowadzono w płycie pręt o sztywności obliczonej zgodnej z zaleceniem normowym dotyczącym przekrojów teowych (wysokość żebra zgodna z rzeczywistością, a szerokość płyty współpracującej b^ = b_w+0,2l_o, co w omawianym przypadku dało wartość b_eff = 0,3+0,2 7,2 = 1,74 m (rys. 2d),

e) płytę w miejscu żebra pogrubioną do 0,94 m, aby otrzymać sztywność żebra zgodną z obliczoną w przypadku żebra w punkcie d)

(rys. 2e),

f) model, w którym pogrubiono płytę w miejscu żebra zgodnie z rzeczywistą wysokością żebra (rys. 2f),

g) model, w którym przyjęto pogrubienie jak w f), zmieniając parametry materiałowe w ten sposób, aby sztywności giętne i skrętne belki były zgodne z zaleceniami normowymi zawartymi w modelu, jak w punkcie d)

(rys. 2g).

Zaletą aproksymowania w modelu stropu 2D belki przez pręt (por. rys. 2d) jest oczywiście dochowanie wprost zaleceń normowych co do sztywności belki. Jednocześnie wadą tego sposobu modelowania jest brak możliwości obliczenia obciążenia ustroju ciężarem własnym, przez obliczenie objętości konstrukcji, a także utrudnienie w uwzględnieniu zwiększonej sztywności płyty na obszarze belki przy wymiarowaniu płyty w kierunku poprzecznym.

Z kolei zaletą pogrubienia płyty do wymiarów belki (por. rys. 2f) jest możliwość bezpośredniego określania ciężaru własnego konstrukcji oraz bezpośrednie zesztywnienie płyty nad belką. Bezsprzeczną wadą jest w tym przypadku jednocześnie zaniżenie sztywności giętnej i skrętnej w stosunku do modelu odniesienia, jakim jest model powłokowy (por. rys. 2a).

Szczególną uwagę zwrócono na model według rys. 2g, jako szczególnie wygodny w modelach płaskich płytowych (2D). W modelu tym belka stanowi pogrubienie płyty do rzeczywistej grubości belki, co pozwala na automatyczne obliczanie ciężaru własnego ustroju, przez lokalne zliczanie objętości konstrukcji i przemnożenie jej przez ciężar właściwy materiału stropu. Jednocześnie w modelu tym cechy wytrzymałościowe są w pełni zachowane, co pozwala, w konsekwencji, na wymiarowanie zbrojenia. Aby mogły być dochowane sztywności giętne i skrętne jak w przypadku belki teowej, z uwzględnieniem szerokości współpracującej płyty, następuje niejawna modyfikacja parametrów odkształceniowych E i G.

W przypadku każdego modelu belek rozważono dwa przypadki:

I - gdy na ścianach podpierających opiera się zarówno żebro, jak i płyta stropowa,

17^ fe

i* zjeiopo

nr

pi

nr

^fKJ.

JjL

nr

Rys. 2. Analizowane modele obliczeniowe (opis w tekście)

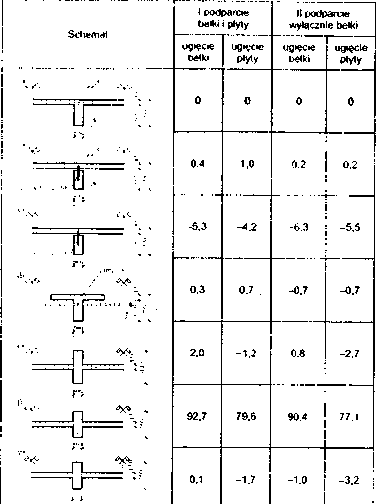
Tablica 1

Schemat belki swobodnie podpartej - wartości odchyleń (%) ugięć w stosunku do modelu powłokowego, w zależności od typu modelu (wartości dodatnie - nadmiar)

II - gdy na ścianach podpierających oparto wyłącznie żebra - krawędź płyty nie jest podparta.

Model powłokowy (por. rys. 2a) odwzorowuje, w sposób dość wierny, sytuację rzeczywistą. Niekonsekwencją tego modelu (pomijając dozwolone normami [2, 3] przyjęcie izotropo-wości i liniowej sprężystości materiału) jest wzajemne zachodzenie na pewnym odcinku

I MM 5(> . .. ^r \.

elementów powłoki poziomej ^ ’: ¹ v =* i pionowej (rys. 3). Z uwagi na

'-—^:-- dużą szerokość współpracują-

i cej płyty, wpływ ten jest

w omawianym przypadku nie-•^: " wielki, tak że w podanych dalej

——i wynikach obliczeń nie stoso-

* ¹"¹’ * wano dodatkowych zabiegów.

Rys 3. W2a,emne zachodzenie Pozwalających na wyelimino-powłok: 1 obszar zachodzenia wanie tego wpływu.

Ponieważ w przypadku I przyjęto w modelu liniowe podparcie płyty i belki, podparcie to zrealizowano w sposób przedstawiony na rys. 4. Chodziło o to, aby nie podpierać płyty na odcinku zajmowanym przez belkę. O takim założeniu podpór należy każdorazowo pamiętać, gdyż w innym przypadku, tj. przy pozostawieniu w modelu podpór przy krawędziach belek, imituje się nieistniejące zawieszenie belek na płycie stropowej. Zaniża to uzyskiwaną wartość reakcji podporowej.

“A A ”j A A

Rys. 4. Sposob realizacji podparcia belki i ptyly

W wyniku przeprowadzonych obliczeń (programy ABC--Obiekt i ABC-Ptyta)¹’, uzyskano, traktując model powłokowy jako model odniesienia, przedstawione w tabl. 1 relatywne różnice ugięć, uzyskane w przypadku poszczególnych modeli. Pozwala to, w przypadku określania ugięć, na oszacowanie stopnia wzajemnej zgodności pomiędzy modelami obliczeniowymi. Jest widoczne, czego można się było z góry spodziewać, że model według rys. 2f (pogrubienie płyty do wysokości belki) obarcza wyniki, w odniesieniu do ugięcia, nieakcepto-walną wartością odchylenia.

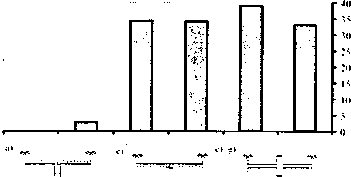
Sposób podparcia belek (sama belka łub jednocześnie belka i płyta) okazał się nieistotny w przypadku obliczania ugięć - maksymalna różnica 1,2%. Tezę tę zweryfikowano dodatkowo nie przedstawionymi tutaj obliczeniami, w których sukcesywnie zmniejszano w modelu wysokość belki według rys. 2a. Natomiast sposób podparcia modelu okazaf się istotny w przypadku rozdziału wartości reakcji otrzymanych, w zaiezności od typu zastosowanego modelu obliczeniowego. Traktując model powłokowy jako modeł odniesienia, uzyskane wartości odchyłek, w przypadku jednoczesnego podparcia belki i płyty, przedstawiono na rys. 5. Jeżeli w modelu obliczeniowym podpierano jedynie belkę, nie wystąpiły, co oczywiste, żadne różnice ze względu na rodzaj modelu.

Jak wyraźnie widać, inaczej reagują na jednoczesne podparcie belki i płyty modele powłokowe (według rys. 2a i b), a inaczej modele płaskie 2D. Można stąd wnosić, że w modelach płaskich następuje wyraźne zaniżenie wartości części reakcji przekazywanej bezpośrednio na płytę. To spostrze-'• Autorem programów jest dr inż. Krzysztof Grajek.

Rys. 5 Wartości odchyleń reakcji przekazywanych na beKe. w :>rzvpadku jednoczesnego podparcia belki i płyty, w stosunku do modelu powiekowego (wanosci dodatnie - nadmiar!

zenie każe inaczej spojrzeć na zbrojenie belek na podporze. Sugeruje konieczność zakładania strzemion w strefie podparcia belek w przypadku, gdy jednocześnie z belką podparta jest płyta stropowa.

Strop dwuprzęsłowy symetryczny poprzecznie nieskończony

Rozważono strop dwuprzęsłowy symetryczny. Zaadaptowano wszystkie modele belek uprzednio omawiane, wprowadzając wynikłe z przepisów normy zmiany w modelu d). e) i g)

INŻYNIERIA I BUDOWNICTWO NR 10.2008 551