Egzam z Żelbetu semestr2 str 0006 bmp

burta

hghp

b_eff/a

kNm

7    6    5    4    3    2    1

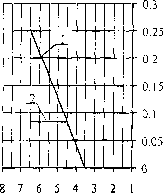
Dla zmiennych wysokości belki (h_b) poszukiwano takiej szerokości efektywnej płyty b_Btl, na której w strefie podporowej nie wystąpiły naprężenia ściskające - wyniki podano na rysunku 5.

£P

Rys. 4. Wewnętrzna belka stropuptytowo-żebrowego (grubość belki b_w=0,4 m, wysokość belki h_b - zmienna, odstęp między belkami a=6 m, grubość płyty h=0,2 m, grubość ścian podpierających b_s=0,25 m, obciążenie g=10 kNIrn¹, beton B25)

Jak widać z rysunku 5, maksymalna szerokość płyty traktowana, przy podanych założeniach, jako współpracująca przy przenoszeniu rozciągać w strefie nadpodporowej, dla hjh > 6,5 wyniosła b_a)l = 0,25x6,0=1,5 m tj. b_in=b_w+5,5 rt_p. Jednocześnie dla hjh < 4,5 cały obszar płyty z boku belki podlegał ściskaniu.

Rys. 5. Stosunek efektywnej szerokości płyty na której nie występują naprężenia ściskające w przekroju nadpodporowym płyty, w stosunku do rozstawu żeber a. 1 - model wg rysunku 3a, 2 - model wg rysunku 3b

Prowadzi to do stwierdzenia, że wpływ naprężeń rozciągających w płycie na wymiarowanie zbrojenia nadpodporowego belek jest, w większości praktycznych przypadków, niewielki. W konsekwencji można uznać, że strefę podporową płyty najwłaściwsze jest wymiarować (na catej jej szerokości) w kierunku równoległym do belki na czyste zginanie. Podejście takie jest technicznie najbardziej sprawne i wynika z dotychczasowych doświadczeń. Przy tym przyjęciu zakładamy, że ewentualny niedobór zbrojenia w partiach płyty przy belce wywołany sitami rozciągającymi, zrównoważony zostanie występującym w tym miejscu większym ramieniem sil wewnętrznych. Dla szczególnych przypadków można prowadzić bardziej precyzyjną analizę.

Strefa przęsłowa

Strefę przęstową analizowano na dwóch, wcześniej opisanych modelach (rys. 4a i b) oraz na modelu stropu z belek jednoprzęslowych (4c). Dla wszystkich trzech stropów określono maksymalną szerokość płyty b_e„, w których na wysokości płyty stropu nie występuje rozciąganie. Wyniki przedstawiono na rysunku 6.

Rys. 6. Stosunek efektywnej szerokości płyty t>_e„ na której nie wys/ę-pują naprężenia rozciągające w przekroju przęslowym, w stosunku do rozstawu żeber a.

1 - model wg rysunku 4a, 2 - model wg rysunku 4b, 3 - model wg rysunku 4c

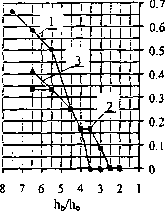
Analizując wyniki obliczeń pokazane na rysunku 6 można stwierdzić, że w przekroju przęstowym w zakresie h_b/h_p < 3,5 obszar ściskania ptyty stropowej ogranicza się wyłącznie do szerokości żebra. Przy większych stosunkach bjh_v, szerokość tego obszaru wyraźnie wzrasta. Aby oszacować udział płyty w przenoszeniu obciążeń przez żebra określono dla modelu jak na rysunku 4c i przedstawiono na rysunku 7, wartości momentów przenoszonych przez samo żebro (wykres 1) i wartości momentów przenoszone przez żebro i współpracującą płytę (wykres 2).

Rys. 7. Wartości momentów zginających przenoszonych przez jednoprzęsiowe żebro stropu wg rysunku 3c, w zależności od stosunku wysokości zebra h_b do grubości płyty stropowej h_c (opis w tek-

^ście>    My

Analiza przedstawionych na rysunku 7 przebiegów wartości momentów w funkcji h,/h wskazuje na to, że udział momentów w płycie wchodzących w zakres oddziaływania żebra jest bardzo maty. W analizowanym przypadku osiągnął on maksymalnie 1,3% całkowitego momentu przenoszonego przez strop. Praktycznie nie należy liczyć na to, że część wykazanych momentów w płycie przejmie żebro.

Skłania to do przyjęcia, że ptytę stropu w obszarze momentów dodatnich działających w kierunku równoległym do żebra, należy zbroić na wartości wykazanych momentów zginających w płycie modelu.

4. Wiarygodność założeń upraszczających

W tradycyjnych obliczeniach, wewnętrzne żebra stropu obciąża się zwykle obciążeniem zebranym z sąsiednich pól, przyjmując jako linie dzielące linie połowiące odległość pomiędzy sąsiednimi żebrami. Przy większych rozstawach żeber stosuje się czasem oszczędnościowe zbieranie obciążeń zgodnie z „regułą dachu”, zakładając, że część obciążeń płyta stropowa przekaże bezpośrednio na podpory. Prowadzi to do trapezowego rozkładu obciążenia żebra. Zbadano dla stropu jak na rysunku 4c, jaki jest stosunek momentów zginających żebro, uzyskanych przy zastosowaniu modelu z elementów powłokowych M do momentów otrzymanych dla wypreparowanych belek statycznie wyznaczalnych obciążonych według obu opisanych sposobów. Jako wartości zmienne przyjęto:

•    hjh (wysokość żebra /grubość płyty);

•    a// (osiowy rozstaw żeber/rozpiętość obliczeniowa żeber).

Rezultaty obliczeń przedstawiono na rysunku 8.

,    7    6    5    4    3    2    1

' Rys, 8. Stosunek momentów zginających żebro, uzyskanych przy zastosowaniu modelu z elementów powłokowych M_fa/ do otrzymanych dla wypreparowanych ze stropu beiek statycznie wyznaczalnych momentów M_m, w zależności od hjh_p Obciążenia wg prostokąta dla a/l=1,5 ; (ozn, 1) i a//=2,0 (ozn. 2), obciążenia wg trapezu dla I a/l=1,5 (ozn. 3) i all=2,0 (ozn. 4).

| Analiza wyników obliczeń zilustrowanych na rysunku 8 wskazuje, że;

• przy założeniu, że obciążenie z płyty przekazywane ! jest na żebro w formie prostokąta, istnieje zawsze mniejsza lub większa rezerwa w wartościach momentów w stosunku do momentów w rzeczywistości przenoszonych przez rozważane żebro (krzywe 3 i 4). i Pamiętać należy dodatkowo, że sztywność żebra podlegać będzie w wyniku obciążenia silniejszej degradacji niż płyta stropowa, W ślad za tym, .rzeczywiste momenty przenoszone przez przekrój żebra ulegną zmniejszeniu;

• przy przyjęciu, że obciążenie z płyty przekazywane jest na żebro w formie trapezu, istnieje przy wysokich żebrach niebezpieczeństwo niedoszacowania wartości momentów działających na żebro.

Wyniki obliczeń przedstawione na rysunku 8 wskazują jednocześnie, że obliczenia klasyczne przy rozłożeniu obciążeń nawet wg prostokąta, przeszacowują dla hjli_p<3,5 wartości obciążeń przejmowanych przez żebra. Tym samym następuje niedoszacowanie wartości momentów przejmowanych przez płytę w kierunku równoległym do długości żeber. Może to prowadzić dla hjh <3fi do niedozbrojenia płyty w kierunku równoległym do długości żeber.

5. Podsumowanie

Wykazano, praktycznie we wszystkich analizowanych sytuacjach, na istnienie konieczności rozróżnienia przy projektowaniu belek „wysokich" o h_b/h_p > 3,5 i belek „niskich” o h₆/h_p < 3. W stosunku do belek wysokich można zakładać, że płyta stropowa się na nich opiera, mogą też być one liczone metodami klasycznymi. Zalecenia normowe [1], odnośnie szerokości współpracującej belek teowych, odnoszą się także do tej klasy belek. Belki niskie stanowią użebrowa-nie płyty i wymagają wnikliwszego podejścia. Wymiarując belki i płyty stropowe na podstawie wyników obliczeń komputerowych, można, bez istotnego błędu, przyjąć niezależne wymiarowanie belek (na uzyskane dla belek wartości sił I momentów) oraz niezależne wymiarowanie zbrojenia płyt (na momenty wykazane w płycie w kierunku równoległym do belek).

BIBLIOGRAFIA

[1]    PN-B-03264;2002 Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i projektowanie

[2]    Rombach G., Anwendung der Finite-Elemente-Methode im Betonbau, Feh!erqueilen und ihre Vermeidung, Ems & Sohn, 2000

[3]    Starosolski W., Aneks do Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, wyd. PRO-SOFT, wersja 3, Gliwice, 2007

www.przegladbudowlanypl/archlwum.html

Archiwum od ręki ,

archiwalne spisy treści i ¹ ' pa stronach www

w    ■ . V. .    9/2008

53