Egzam z Żelbetu semestr2 str 0004 bmp

{rys. 6a), co przedstawiono na rys. 6b i c. Przyjęto jednoczesne podparcie belki i płyty. Wartości momentów zginających podporowych i sił poprzecznych określono w odległości 0,15 m od osi podpory wewnętrznej, na krawędzi podparcia. Uzyskane w wyniku przeprowadzonych obliczeń wartości zestawiono w tabl. 2.

.    nbN/;n I    Ohs/arll    (>fcs/ar I

Strop ciągły - przęsło wewnętrzne

Analogicznie jak uprzednio, analizowano sytuację przęsła wewnętrznego stropu ciągłego. Uwzględniono wszystkie uprzednio omawiane modele belek, wprowadzając wynikłe z przepisów normy zmiany w modelu wg rys. 2 d, e i g. co pokazano na rys. 7.

a)    Obs/arll    (>hs/;if I    <»h>/arll

1200 j, 12CKI ^    4X00    ^ 1200 1200 ^

7200

_; 12(Mr 1200^    MKKI

72<H)    |    72<M)

5.52 (Obszar I) 0.73 (Obszar II)

□.....;,_f

300    ™ 5

1,31 (Obs/ai I) 0.73 (Obs/ar II)

•300

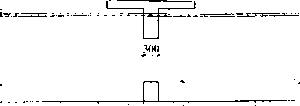
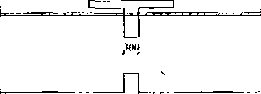
Rys. 6. Modele typu d) i e) w przypadku belki dwuprzęsłowej: a) przekrój podłużny - obszary I i II. b) dane do modeli d) i g). c) dane do modeli e)

Tablica 2

Schemat belki dwuprzęsłowej - wartości odchyleń (%) w stosunku do modelu powłokowego: momentów zginających, sit poprzecznych i ugięć w zależności od typu modelu belki (wartości dodatnie - nadmiar)

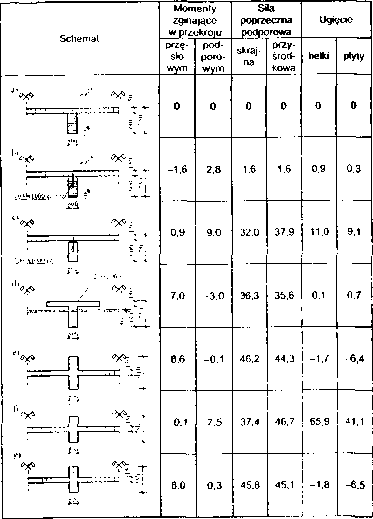
Rys. 7. Modele typu d). g) i e) w przypadku przęsła wewnętrznego belki ciągłej nieskończonej: a) przekrój podłużny - obszary I i II. b) dane do modeli d) i g), c) dane do modeli e)

Wartości momentów zginających podporowych określono na krawędzi podparcia, w odległości 0,15 m od osi podpory wewnętrznej. Wyniki obliczeń podano w tabl. 3.

W obu przypadkach (tabl. 2 i 3) belek ciągłych będących częścią stropu uzyskaliśmy, w stosunku do momentów podporowych, potwierdzenie prawidłowości zalecanych przez normę szerokości płyty współpracującej z betką. Jednocześnie stosowanie tych zaleceń prowadziło, w każdym razie w sprawdzanym zakresie, do zawyżenia przęsłowycłi wartości momentów zginających o kilka do kilkunastu procent. W każdym przypadku uzyskane wartości lokują się po stronie bezpiecznej.

Potwierdzono, czego należało się spodziewać, że modele typu d), e) i g) są modelami praktycznie równorzędnymi, ale tylko wtedy, gdy (co omówiono dalej) na belkę nie działają momenty skręcające.

Modelowanie belki przez pogrubienie płyty do wartości rzeczywistych wymiarów belki (według rys. 2f) prowadziło do zgodnych z modelem powłokowym wartości momentów w przęśle i jedynie kilkuprocentowego ich zawyżenia na podporze.

Żebra skrajne

Powyższe analizy przedstawiały sytuację żebra wewnętrznego stropu poprzecznie nieskończonego. Niżej przedstawiono, w ograniczonym zakresie, jaki jest wpływ zastosowanego modelu belki na wyniki obliczeń, przy ograniczonej szerokości stropu i przy istotnym wpływie żebra skrajnego.

Przyjęto we wszystkich analizowanych sytuacjach jednakowe założenia: płyta grubości 0,20 m, belki o przekroju 1,4 x 0,4 m w rozstawie co 6,0 m, długość belek 18 m, obciążenie równomierne 10 kN/m². We wszystkich sytuacjach podpierano w modelu zarówno belkę, jak i płytę wzdłuż krawędzi poprzecznych do długości belki. W przypadku modelu powłokowego, wzdłuż podpór wprowadzono poprzecznicę grubości 0,2 m.

Rozważono cztery typy modeli zarówno stropu jedno-, jak i dwuprzęsłowego:

552

INŻYNIERIA I BUDOWNICTWO NR 10/2006

Tablica 3

Schemat belki ciągle) - wartości odchyleń (%) w stosunku do modelu powłokowego: momentów zginających, sil poprzecznych i ugięć, w zależności od typu modelu (wartości dodatnie - nadmiar)

	Schemat		Momenty zginające w przekroju		Siła poprze-	Ugięcie
			przęsło- wym	podpo rowym	podpo rowa	belki	płyty
		-V • .		0	0	0
	y,
"V			0.3	0	0,7	1,7	1.1
........	.......ii.
^C,'V*			4.5		38.3	-15.7	-10.6
	........i^1 2 3 4;
V	/ /		13,6	-1.2	39,0	-5.8	—4.1
	■T^1-
	/•"i
	n		14.5	2,0	50.0	-5.7	-10.9
	u
	. n	^ -	2.0	5.4	48.2	45,5	22.3
	u	-
-U- "i			13,9	2,0	50,0	-7,2	-11,9

Tablica 4

Wartości odchyleń (%) momentów zginających dodatnich w przekroju środkowym w belkach modeli jedno- i dwuprzęsłowych w stosunku do modelu powłokowego, w zależności od typu modelu (wartości dodatnie - nadmiar)

Typ modelu	Belka	Strop jednoprzęsłowy	Strop dwuprzęsłowy 0
1. Łupina (rys. 2a)	wewnętrzna	0
	skrajna	0	0
	wewnętrzna	1,4	-0,1
(rys. 2d)	skrajna	-1,8	-1,8
3. Płyta z pogru-	wewnętrzna	-2,1	-2,2
bieniami (rys 2e)	skrajna	20.5	11.9
4. Płyta z belkami	wewnętrzna	0.8	-0,6
(rys 21)	skrajna	^50	5,7

Jeżeli jednak oblicza się belki skrajne, to nawet w przypadku stropów pracujących jednokierunkowo należy modelować belki jako teowe, uwzględniając (przy kształcie według zaleceń normy) zarówno ich pionową sztywność giętną, jak i ich sztywność skrętną.

Rozkład reakcji jest, w sposób bardzo silny i chimeryczny, uzależniony od zastosowanego modelu szczegółowego i podparcia płyty obok żebra. Przeprowadzona analiza wskazała, że przy tradycyjnych przyjęciach nie docenia się zwykle wartości sil przekazywanych na podpory przez podpartą z boku belki płytę.

Podsumowanie

Przedstawione obliczenia, z konieczności ograniczone, zwracają uwagę przede wszystkim na to. że do modelowania ustrojów, nawet przyjmując izotropię i liniową sprężystość materiału, podchodzić należy zawsze z rozwagą. Wskazują też na konieczność zachowania krytycyzmu wobec uzyskanych wartości, które są jedynie oszacowaniami o większej lub mniejszej wiarygodności.

Podane wyniki obliczeń mogą być wskazówką w odniesieniu do kształtowania modelu obliczeniowego. Wskazują kiedy -jest możliwe modelowanie belek w sposób bardzo elementarny, a kiedy trzeba sięgać po bardziej złożone ich kształtowanie.

Spośród przedstawionych różnych sposobów modelowania belek jako najwłaściwszy, bo łączący prostotę kształtowania z dużą poprawnością wyników, należy uznać, zdaniem autora, modelowanie belek według założeń schematu rys. 2g (stosowany między innymi w programie ABC-Płyta). Zachowuje się w tym przypadku jawnie wymiary żebra prostokątnego, jako pogrubienia płyty, uwzględniając w sposób niejawny jego teowy kształt, wpływający zarówno na sztywność giętną. jak i skrętną żebra.

PIŚMIENNICTWO

[1]    Avak R., Goris A : Stahlbetonbau aktueil. Pra*rshandbuch 2004. Bauwęrk. Berlin 2004.

[2)    PN-B-03264 2302 Konstrukcje betonowe, żelbetowe i sprężone - Obliczenia statyczne .'•••o-ektowanie.

[3} PN-EN 1992 ’•* Eurokoo 2: Projektowanie r (instrukcji z betonu Część 1-1: Reguły o?**;.-w i reguły dla budynków.

(4)    Rombach G.' Anwenoung der Finiłe-Elemente-Methode im BeKrnau. Fehlerquellen i.-d ihre Vermeidung. Erns & Sono. 2000.

[5]    Siarosoiski W Aneks do ..Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich". PR0-S0F7. wersja 3. Gliwice 2007.

[6| Staro$ol$ki W : O -ozmeszczaniu obciążeń zmiennych w stropach t 'ryzo wo-zbrojonycr • pfytowo-slupowych. Jnzyręna i Budownir !*,?    ' •

4/2008.

553

INŻYNIERIA I BUOOWNICTWO NR 10/2008

1

   - strop jako powłoka,

2

   - strop jako płyta, w którą wprowadzono belki w postaci prętów (belki wewnętrzne o szerokości współpracującej płyty 0,4 + 0,2 • 18 = 4 m i belki skrajne o szerokości płyty współpracującej 0,4 + 0,1 • 18 = 2,2 m),

3

   - strop jako płyta z pogrubieniem do 1,4 m, odpowiednio na szerokości żeber,

4

   - strop jako płyta z pogrubieniem do 1,4 m, odpowiednio na szerokości żeber, ale z niejawnym uwzględnieniem szerokości współpracującej płyty, jak w przypadku 2.

Wyniki obliczeń zestawiono w tabl. 4 (więcej informacji w [5]).

Przeprowadzone obliczenia, poparte także innymi o szerszym zakresie, pozwalają na potwierdzenie znanej tezy, że przy modelowaniu belek wewnętrznych stropów jednokierunkowo pracujących nie wprowadza się istotnego błędu w obliczenie momentów zginających, traktując belki jako lokalne pogrubienia stropu, o wartości zgodnej z wysokością rzeczywistą tych belek. Stosując w obliczeniach ten model belki, należy się liczyć z formalnie kilkuprocentowym niedomiarem zbrojenia na podporze. Jednocześnie obok belki musi w rzeczywistości przebiegać nadpodporowe zbrojenie płyty, zwykle pokrywające z nawiązką wykazany w belce niedomiar.

Trzeba mieć świadomość, że powyższe stwierdzenie zachowuje ważność jedynie przy tradycyjnych proporcjach płyt i belek i nie jest ważne w odniesieniu do stropów krzyżowo zbrojonych [6]. Omówione przyjęcie skutkuje jednak dużym błędem przy określaniu ugięć. W celu uzyskania prawidłowych ugięć pogrubienie płyty powinno odpowiadać giętnej sztywności bełki teowej, obliczonej według zaleceń normowych.