HWScan00065

AKCJI 1 OBLIGACJI - Teoria, pytania, zadania

dr Adam Bartmbruch. abartmbruchd,»zr pi

[6] STOPA DOCHODU OBLIGACJI - ZADANIA

6.1 Nominalna I bieżąca stopa zwrotu z obligacji

(Przykład) Obligacja trzyłatnia wartośd nominalna] 100,00 PIN, o kuponach odsetkowych wypłacanych oo rok wynoszących 5,00 PLN, notowana po kunia 98,38%. Od ostatnie] wypłaty odsetek upłynął kwartał. Podstawowe parametry takiej obłlgacjl:

Cena rynkowa (czysta): 98,38%x100,00*98,38 PLN Cena rynkowa (brudna): 98.38*0,25x6,00*99.63 PLN

ą 00

r, - — xl00°o-5,00^#o Rentowność nominalna:    ¹ ^ ^Cj

r_} »-l^*100*.= 5,08*o Rentowność bieżąca:    98,38

Obliczone powyżej parametry nie wystarczą aby określić rentowność inwestycji w obligacją w pełnym jej okresie ani ceny, którą należy —uzyskać zakładaną rentowność. Niezbędna jest więc korzystania z bardziej zaawansowanych obliczać.

ile wynosi nominalne stopa zwrotu oraz bieżąca stopa zwrotu piętnastoletniej obligacji kuponowej o towaniu 7% rocznie, wartości nominalnej 1000 zł i cenie 769,40

r. = —x 100°«	rr =-Lxl00^a«
P

Pyt 2 Ile wynosi stopa zwrotu w terminie do wykupu dla obligacji zerokuponowej dwudziestoletniej o wartości nominalnej 1000 zł sprzedawanej po 439,18 zł.

| 6.2 Stopa zwrotu z obligacji w okresie do wykupu_

Pyt 3 Dana jest obligacja z terminem wykupu 3 lata, wartość nominalna obligacji wynosi 1000 zł, oprocentowanie ^/6%^sbd setki płacone co roku. Cena tej obligacji na rynku wynosi 976. Wyznacz stopę dochodu z tej obligacji w terminie do wykupu (YTM)

Pyt 4 Dana jest obligacja z terminem wykupu 3 lata, wartość nominalna obligacji wynosi 1000 zł. oprocentowanie 6%, odsetki płacone co pół roku. Cena tej obligacji na rynku wynosi 976. Wyznacz stopę dochodu z tej obligacji w terminie do wykupu (YTM)

Pyt 6 Dana jest obligacja zerokuponowa o terminie wykupu 2 lata, wartości nominalnej 1000 zł i o cenie 926 zł. Wyznacz stopę dochodu obligacji w terminie do wykupu

Pyt 6 Dane są trzy obligacje skarbowe o wartości nominalnej 1000 zł o odsetkach płaconych raz w roku. Stopa dochodu wszystkich obligacji jest jednakowa i wynosi 5%. Charakterystyki obligacji są następujące

Obligacja X - 3 lata do wykupu, oprocentowanie 6% Obligacja V - 4 lata do wykupu, oprocentowanie 6% Obligacja Z - 3 lata do wykupu, oprocentowanie 5%

1-

1

PV = PVA. = PMT

(1 + r)"

Czy zoadzaszsłę z poniższymi sNśerdzenłami?_

Obligacja X jest mniej wrażliwa w sensie zmiany ceny niż obligacja Y, która ma krótszy termin wykupu

Obligacja X jest mniej wrażliwa w sensie zmiany ceny niż obligacja Z, gdyż ma wyższe oprocentowanie_

Pyt 7 Dana jest obligacja o następujących parametrach: oprocentowanie obligacji 8%. czas trwania obligacji 25 lat. odsetki wypłacane co pół roku. Oblicz a następnie przedstaw na wykresie

Obiła wartości bzach obtgacji przy zmianie wymaganej stopy dochodu o _+/-1 punkt procentowy

a)    Wartość nominalną obligacji

b)    Zgromadzony kapitał z tytułu zakupu obligacji (bez reinwestycji odsetek) - efekt zysku z odsetek na odsetkach i jego wpływ na wartość końcową inwestycji w obligację

c)    Zgromadzony kapitał z tytułu zakupu obligacji zakładając stopę reinwestycji na poziomie 8% w skali roku

d)    Oszacuj stopę zwrotu z inwestycji przy braku reinwestycji i przy jej zastosowaniu

l 6.3 Stopa zwrotu w okrasie wezwania do wykupu_

Pyt 8 Dana jest obligacja z terminem wykupu 3 lata, której wartość nominalna wynosi 1000 zł. oprocentowanie 6%, a odsetki płacone są po roku. Cena tej obligacji na rynku wynosi 976. Stopa dochodu tej obligacji wynosi 6,91%. Załóżmy, że jest to obligacja typu callable w przypadku której wcześniejszy wykup może być dokonany najwcześniej po pierwszym roku po cenie 1000 zł. Wyznacz stopę YTC (yield to cali)

Pyt 9 Dana jest obligacja z terminem wykupu 3 lata. której wartość nominalna wynosi 1000 zł, oprocentowanie 6%. a odsetki płacone są po roku. Cena tej obligacji na rynku wynosi 976. Stopa dochodu tej obligacji wynosi 6.91% Załóżmy, że jest to obligacja typu putable w przypadku której wcześniejszy wykup może być dokonany najwcześniej po drugim roku po cenie 1000 zł Wyznacz stopę YTP (yield to put)

■

dr Adam Bart mb nich, obartmbmchajyzr pi

6.4 Stopa zwrotu i portfela obligacji

Rozważmy portfel inwestycyjny składający się z trzech obligacji

/ Ottigażja	Oprocentowanie	Okres do wykupu	Wartość nominalna	Cena	Stopa wrotuw terminie do wykupu
~	0,07	5	10000	9209	0,09
B	0,106	7	20000	20000	0,105
C	0.06	3	30000	28050	0.066

Przyjmijmy, że data płatności odsetek jaat Jednakowa dta każdej obligacji (oo pół roku). Ha wynoai całkowita wartość rynkorraportfejitf Uzteelnii tabelę o przapływy gotówkowa z każdej obłipadlcaleoo portfela._^ ■ ■&*)

0.035

0,0525

0.03

9209

20000

28060

57259

Okraa

2frę>.

3^0

mlin

Anm

Top

Portfal

-Aj) OO

3)0

btp

3To~

ifo

JOc2_

-iSja.

.10 Łflł.

-M-

AÓŚo

A2Ś?

.A222.,

Aóso

A O to

MSO

AlcfO

9o£_

35

O-

hOSOO

.223X2.

23 30

*2 bo o

2bop_

3Z joc>

/fl/CtO

/iuoo

AAUDo_

AQ5o.

A OŚO

Aoso

Aby okraślć stopę zwrotu z całego portfela, należy znaleźć taką stopę procentową, dla której wartość obecna przepływów gotówkowych przedstawionych w _tabak równa się catandtaj wartości portfela (57.259). Warunek ten spełniony jest dta stopy procentowej równaj 4,77%08a półrocza)

fj, V. iOoO Jo

aoo'/

Ą330

4,3/

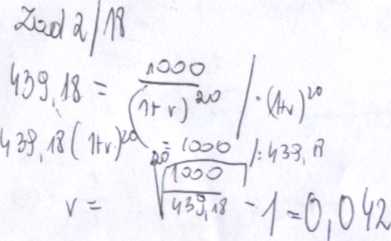
la-~l A —

O j cA

J

^ty ** ^C

19