Image0007 BMP

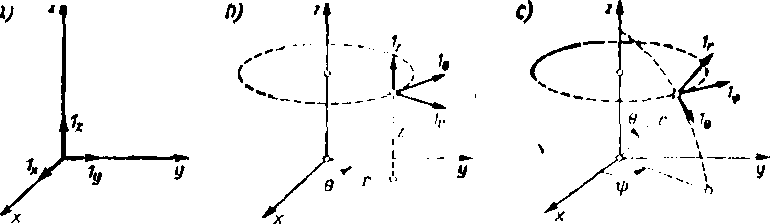
ys. 1.1. Wersory w układzie współrzędnych prostokątnych (a), w uklacl/ic współrzędnych .walcowych (b) oraz w^, układzie współrzędnych kulistych (c)

s. l.lc). Wektor A w układzie współrzędnych prostokątnych można przedstawić w poci

A^A^+Arly+Ath.    (1-1)

Iloczyn wektora A o składowych A_x, A,., A. przez skalar X jest wektorem AA o skła-.vych X,A_xt XA_y, XA_Z.

.2. Funkcja wektorowa. Pole wektorowe

Przypuśćmy, że w każdym punkcie obszaru v określony jest wektor A, wobec czego on funkcją trzech zmiennych przestrzennych .r, y, z, czyli A (jc, y, z). W ogólnym ypadku wektor A może zależeć jeszcze od czasu /. Otrzymuje się w ten sposób funkcję ■torową A (*, y, z, t), która jest równoważna trzem funkcjom skalarnym: A_x (jt, y, ), A_y(x,y, z, t) oraz A_t(x, y, z, t), przedstawiającym poszczególne składowe wek-t. Funkcja wektorowa określona w pewnym obszarze przedstawia pole wektorowe yrn obszarze. Funkcję wektorową A (jc, y, z, t) będziemy często oznaczać A (P, i), ie P jest punktem o współrzędnych jt, y, r.

Unią pola wektorowego lub krótko linią pola nazywamy krzywą, której styczna ma unek wektora pola w tym punkcie. Polem równomiernym nazywamy pole, w którym tor pola jest stały, czyli ma stalą wartość liczbową (miarę) oraz stały kierunek i zwrot, ie pola równoramiennego są prostymi równoległymi.

1. Iloczyn skalarny i wektorowy

loczynem skalarnym AB wektorów A i B nazywamy skalar równy iloczynowi ich ości (miar) przez cosinus najmniejszego kąta zawartego między tymi wektorami,

A-B = /1Bcosk.    (1.2)

bólem mnożenia skalarnego jest kropka. Iloczyn skalarny wektorów prostopadłych ly jest zeru.

locz.yn skalarny podlega prawu przemienności, wobec czego

Wctsory w uKłud/ir współrzędnych pro-itokątnych mają następuj qcc właściwo**:

1, 1.-S I, -i,

(1.4)

l‘i/y wykorzystaniu tych zależności łatwo udowadnia się, że iloczyn skalarny wektorów A i H wyra Aa się wzorem

AB = A_xB_K + A,B_r + A_tB_x.    (1.5)

Kwndial wektora określony jest wzorem:

A² = A • A = /4² +A* + A*.    (1.6)

W-iirow (miara) wektora jest równa

A — | A| = s/A • A = \ł A² + Ay + Ay    (1-7)

i odpowiada długości wektora.

Iloczynem wektorowym A x B wektorów A i B nazywamy wektor, o wartości (mierze) mwnej polu równolcgloboku rozpiętego na wektorach A i B, o kierunku prostopadłym dn lycti wek torii w oraz o zwrocie przyjętym w ten sposób, aby wektory A, B i AxB two-Myly układ prawoskrętny (rys. 1.2). Wartość (miara) iloczynu wektorowego jest równa

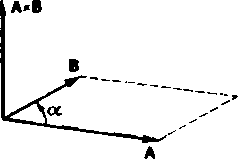
Rys. 1.2. Określenie zwrotu iloczynu wektorowego

AN»in a, przy czym a jest najmniejszym kątem zawartym między wektorem A a B. Sym-bolem mnożenia wektorowego jest krzyżyk.

Iloczyn wektorowy nie podlega prawu przemienności, bowiem

AxB=—BxA.    (1.8)

Wersory w układzie współrzędnych prostokątnych mają następujące właściwości:

l*xlj=lyX l_J1=l_Ixl_I = 0,

* « ^{X —} I, X l_t= I. ,

1,^ I.--1,X1, = 1_JC.    ^{(I 9)}

I*t zy zastosowaniu tyd» zależności łatwo obliczyć iloczyn wektorowy A x B w układzie w ąmlrzędnych prostokątnych; w wyniku utrzymuje się

A x B~(.i_r/J_t- A, B,) 1, f(A. B_x~ A_x flj I, t-(A_xB_r~A_y B_x) I,,    (UO)

I «