img006

44    3. Przekształtniki o komutacji sieciowej

Pomijając składową pracy jałowej w prądzie pierwotnym transformatora, uzyskuje się prostą zależność na wartość skuteczną prądu pierwotnego

h

lub

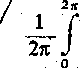
(i-h?

(3.13)

i ■'* 'i.-    ..    2*

h

sin9d3+J /_d ds] =1,21 I_a (3.14) o    o    o

Z powyższych równań otrzymuje się zależności na moce obliczeniowe uzwojenia wtórnego i uzwojenia pierwotnego transformatora

S, = Ul = 3,49Pj    (3.15)

S_p - U_pI_p = 2,69P_d    (3.16)

Moc obliczeniową (gabarytową) transformatora przyjęto określać jako średnią arytmetyczną mocy uzwojenia wtórnego i uzwojenia pierwotnego

S +S

S_t =    = 3,09P_d    (3.17)

Jak wynika ze wzoru (3.17), moc pozorna transformatora zasilającego prostownik jednopulsowy jest ponad trzykrotnie większa od mocy prądu stałego, co świadczy o nieekonomicznym wyzyskaniu miedzi i stali w transformatorze.

Napięcie wyprostowane jest okresową funkcją czasu «j(f) = «j(/ 4- T), przy czym T = 2n/co, i dlatego jego przebieg czasowy można rozwinąć w szereg trygonometryczny Fouriera, zgodnie z zależnością 00 00

u/t) = B₀ + A_n sinnu>t+ B„ cosna>t    (3.18)

n=l    »=1

W wyniku obliczenia współczynników A„ i B„ szeregu Fouriera otrzymuje się

ujifj — l/l/2 I J-+-—-sincot—^-•^-cos2mt—

[_ JC    2    ... ■ ' jr ■■ 3

2    1    1 rr T ,    •

—tz TF^cos^^<at ••• ⁼ l+^sin mt-r-

-

2 2 -y COS 2(Ot--jy COS 4(Ot

(3.19)

Zauważmy, że wyraz B₀ występujący w równaniu (3.18) i wyrażający składową stałą przebiegu okresowego, oznacza tut średnią wartość napięcia wyprostowanego.