img011

50    3. Przekształtniki o komutacji sieciowej

W wyniku rozwiązania równania (3.37) otrzymuje się

h =    l/^+CmĆFCl ~ cos A)    (3.38)

Z równania (3.38) wynika, że gdy C -*• 0, to I_a dąży do wartości określonej zależnością (3.10).

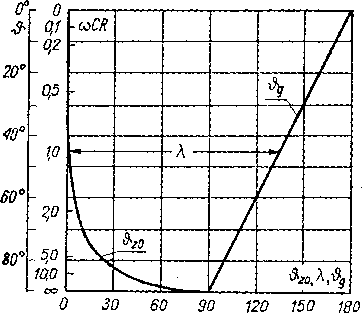
Rys. 3.6. Zależność kątów 9_z0, 9, i źjod parametru mCR dla układu z rys. 3.5

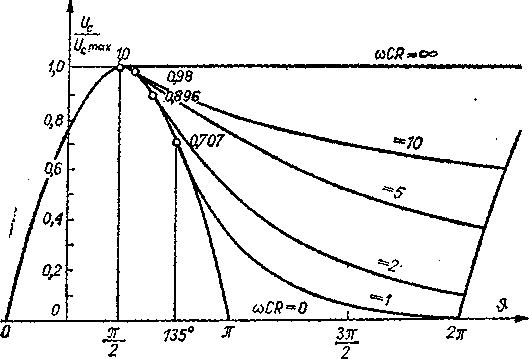
Rys. 3.7. Przebiegi wartości chwilowej napięcia na kondensatorze w funkcji parametru coCR, w układzie z rys. 3.5

W drugim granicznym przypadku, gdy R ~+ 0 otrzymuje się, że -> tc/2, A -> 0, a kondensator ładuje się do napięcia szczytowego źródła zasilającego.