s2 zad13 s2

Drgania wymuszone belki dwuprzęsłowej z dwoma źródłami wymuszenia

Dla <Umej belki z rys. s.10 z dwoma silnikami będącymi s rodłami wymuszenia, pracującymi oddzielnie lub równocześnie, przy różnych fazach pracy silników wyznaczymy obwiednię momentów zginających wywołanych obciążeniem dynamicznym.

Dla układu o LSSD — 2 mamy dwie masy skupione na środkach obu przęseł mi =    = mi, + m_s, pochodzące od ciężaru belki i silników.

»)    4    -k

f P°sin0l    f P°sin6t

A_Bci*_C__-⁴’

A    A m_b+m® (2) A

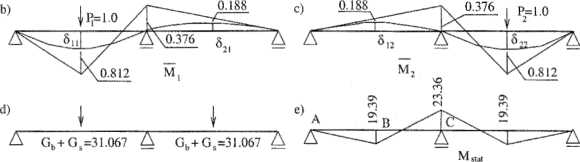
Rys. 8.10. Drgania wymuszone belki o LSSD=2 z dwoma silnikami

W przykładzie przyjmiemy następujące dane szczegółowe: długość każdego przęsła L = 4.0 m, przekrój belki dwuteowy 1300, /r = 0.0544 kNs²/m², masa skupiona na środku przęsła mj = f.iL/2 =    0.109 kNs²/m,

odpowiadająca ciężarowi Gt, =    1.067 kN, E = 2.1 • 10⁸ kN/m²,

/ = 9.8 • 10^-5 ni⁴, El = 20.58 • 10³ kNm², ciężar silnika G_s = 30.0 kN, masa silnika m_s = G_s/g = 3.058 kNs²/m, ciężar wirnika G_w = 10.0 kN, masa wirnika m_w = G_w/g = 1.02 kNs²/m, mimośród awaryjny < = 0.001 m, ilość obrotów silnika na minutę n = 850 min^-1, / = 14.17 s^-1 = 14.17 Hz, częstość kątowa siły wzbudzającej 6 = 2nn/60 = 89.0 s^-1.

Na rys. 8.10b,c pokazaliśmy linie ugięcia i wykresy momentów od jednostkowych sił przyłożonych w punktach położenia mas skupionych. Wykorzystujemy je do analizy statycznej i dynamicznej belki o LSSD — 2.

Od statycznie działających ciężarów belki Gt, i silników G_s powstają w belce momenty zginające pokazane na rys. 8.10e.

Z rozwiązania problemu drgań własnych, opisanego w p. 8.2.3, przy masach

= ni2 = mt, + m_s, znamy dwie częstości kołowe

uą = 69.83 s^-1, w₂ = 105.80 s^-1.

Przyjęta częstość kołowa wymuszenia S = 89.0 s^-1 jest więc odległa od częstości kołowych drgań własnych oi,, i = 1,2.