Str 020

Pole to zostało podzielone na elementarne poletka, tak aby ciśnienie działające na poszczególne poletko było stałe. Są to poziome paseczki o nieskończenie małej szerokości, leżące na głębokości h. Ich powierzchnie równe są d F.

Parcie na taki element wyniesie

dP = p dF = (p₀ + y h) dF.

Wobec tego parcie całkowite jest równe

P = f dP = f (p₀ + yh)dF = p₀F + y J h dF.

F    F    F

Występująca w równaniu całka j" hdF wyraża moment statyczny pola F

F

i może być zastąpiona przez iloczyn h_sF, gdzie h_s jest zagłębieniem środka ciężkości pola F

P = p₀F + yh_sF = y

Po

{ Y

*h.

Jeżeli ciśnienie na powierzchni p₀ równe jest atmosferycznemu, to możemy je pominąć w obliczeniach, równoważone jest ono bowiem ciśnieniem działającym na zbiornik z zewnątrz.

Natomiast, jeśli p₀ wyraża pewne nadciśnienie, możemy jego wpływ zastąpić przez zwiększenie zagłębienia h_s o wielkość wysokości tego nadciśnienia

—, to znaczy umownie podnieść zwierciadło cieczy o wielkość — i przyjąć Y    Y

na tej podniesionej powierzchni cieczy nadciśnienie równe 0.

Podobna metoda zastępowania nadciśnienia na powierzchni przez równoważną warstwę cieczy może być stosowana we wszystkich rozważaniach hydrauliki.

Podany wzór pozwala na obliczenie wielkości parcia, natomiast nie daje możliwości wyznaczenia położenia tego wektora, co w większości zadań jest rzeczą konieczną.

Wypadkowa parcia hydrostatycznego skierowana jest prostopadle do powierzchni i przechodzi przez punkt C położony w odległości y_c oraz x_c od środka ciężkości tej powierzchni S. Osie x i y wzajemnie prostopadłe przechodzą przez środek ciężkości 5, przy czym oś x jest skierowana poziomo (rys. 2.4). Wielkości y_c i x_c obliczyć można za pomocą wzorów:

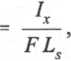
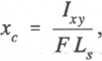
gdzie: L_s - odległość środka ciężkości ściany od powierzchni, na której p - 0, mierzona po powierzchni ściany,

20