P1080226

4. Wprowadzenie do kinematyki robotów

Wartości /, (Poraź O można obliczyć z zależności

1 — +(^4 —1\)*	(4.28)
sin 0 = ——— /	(4.29)
cos &=—	(4.30)

/

Pokazany przykład jest nieskomplikowany, ale realistyczny. Układ sterowania robota powinien wykonywać obliczenia możliwie szybko, gdyż jest to konieczne do uzyskania odpowiedniej płynności działania robota - obliczenia muszą więc być względnie nieskomplikowane. Trzeba zauważyć, że w powyższym rozumowaniu rozdzielono orientację w przestrzeni od pozycjonowania ramienia, co bardzo upraszcza osiągnięcie właściwego rozwiązania.

4.2.4. Opis kinematyki w notacji Denavita-Hartenberga

Dla robotów o wielu stopniach swobody wyznaczenie prostego lub odwrotnego zapisu kinematyki ruchu manipulatora, wykorzystujące równania algebraiczne, jest zadaniem bardzo pracochłonnym, a z punktu widzenia nakładu pracy - zupełnie nieefektywnym. W celu opisania przemieszczeń, prędkości i przyspieszeń układów kinematycznych, wykonujących złożone ruchy w przestrzeni, stosuje się aparat matematyczny umożliwiający przede wszystkim efektywne obliczenia. Dlatego najwłaściwsze jest podejście macierzowe, które pozwala w sposób jednolity i zwarty formalnie przedstawić problemy związane z mechaniką robota, tzn. opis geometrycznych, kinematycznych i dynamicznych związków między członami manipulatora i obiektami manipulacji oraz algorytmy sterowania. Takim właśnie podejściem jest notacja Denavita-Hartenberga o następujących założeniach:

-    robot jest złożony z n członów numerowanych od 0 do n, poczynając od podstawy; podstawę oznacza się jako człon 0;

-    przeguby robota numeruje się od 1 do n, stosując zasadę, że przegub oznaczony jako i łączy człon / - lz członem z;

-    zmienną przegubową oznacza się parametrem #,•; dla przegubów o ruchu postępowym opisuje ona przemieszczenie, a dla przegubów obrotowych - kąt obrotu;

-    do każdego członu należy przyłączyć układ współrzędnych, gdzie podstawę bazową oznacza się jako 0, kolejne zaś układy numeruje od 1 do /z, pamiętając, że układ i jest sztywno połączony z członem /;

-    tworzona jest macierz przekształceń jednorodnych oznaczona jako Ab gdzie punkty z układu / są transformowane do wcześniej opisanego układu i — 1; należy pamiętać, że wartości macierzy A/ zmieniają się

_dynamicznie wraz ze zmianą położenia robota w przestrzeni roboczej.

4.2.4.1. Transformacja prosta w notacji Denavita-Hartenberga

Kinematykę każdego robota można określić na podstawie czterech parametrów, które zostały opisane w notacji Denavita-Hartenberga; są to:

-    długość członu a/_i,

-    kąt skręcenia członu ai~\,

-    odsunięcie członu d_t,

-    kąt konfiguracji #.

Pierwsze dwa parametry opisują człon / — 1, a dwa kolejne połączenie członu z sąsiednim członem i — rys. 4.14.

N rysunku 4.14 przedstawiono człon i - 1 oraz prostą obustronnie prostopadłą do osi dwóch przegubów. Długość członu <?,•_ i mierzy się od punktu przecięcia się prostej obustronnie prostopadłej z osią i — 1 do punktu przecięcia się prostej obustronnie prostopadłej z osią /. Kąt skręcenia członu \ określa względne usytuowanie osi i oraz osi i — 1. Jeżeli wyobrazimy sobie płaszczyznę, której normalna odpowiada prostej obustronnie prostopadłej, a następnie zrzutujemy obie osie na tę płaszczyznę, to możemy zmierzyć kąt zawarty między nimi. Kąt ten jest mierzony w kierunku od osi i — 1 do osi /, zgodnie z regułą prawej ręki wokół prostej a#_|. Dwa współpracujące ze sobą człony mają wspólną oś połączenia ruchowego. Odsunięcie członu di jest to odległość między dwoma członami mierzona wzdłuż ich wspólnej osi. Kąt konfiguracji 0_t członów połączenia ruchowego określa się wartością kąta obrotu wokół wspólnej osi, o jaki obrócono względem siebie sąsiadujące człony.

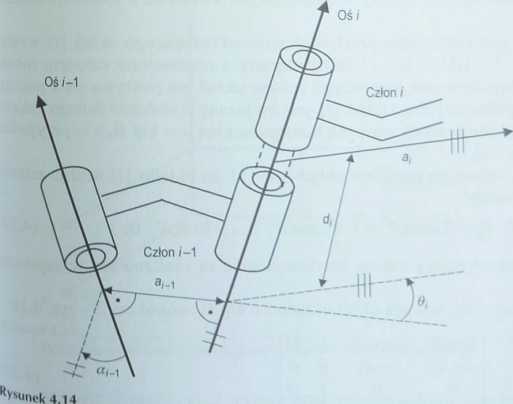
Oznaczenia parametrów stosowanych w notacji Denavita-Hartenberga

99