HPIM0796

4. Wprowadzenie do kinematyki robotów

Wartości /, </>oraz (9 można obliczyć z zależności
l^si]x^:4+y}+(u-l\)^2	(4.28)
sinfls ' -	(4.29)
cos 0=-y-	(4.30)
Pokazany przykład jest nieskomplikowany, ale realistyczny. Układ stero-

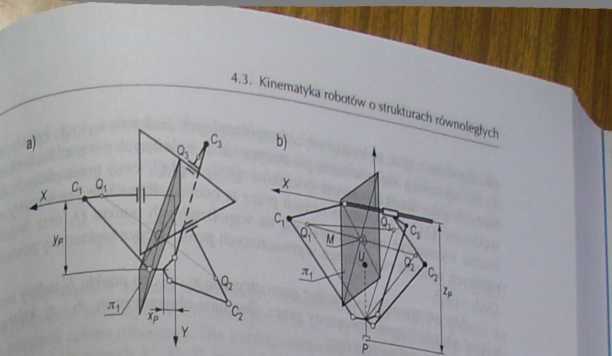
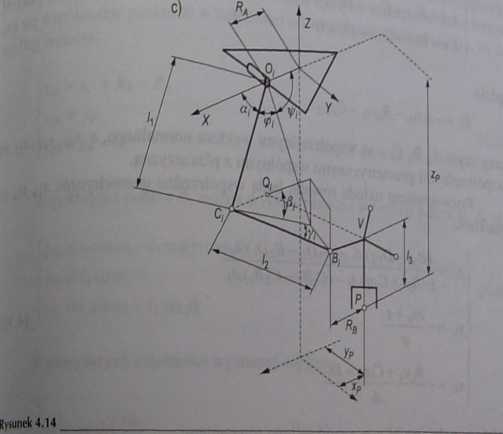
Schemat manipulatora typu DELTA: a) widok z góry, b) widok z boku, c) schemat jednego ramienia układu; | - długość ramienia, - długość członu równoległoboku, /₃ - odległość środka członu roboczego od środka platformy, ą - zmienny kąt obrotu /-tego ramienia, A 1 kąt między płaszczyzną /-tego równoległoboku a płaszczyzną postawy mierzony W płaszczyźnie pionowej, zawierającej /-te ramię, # - kąt między płaszczyzną pionową /-tego ramienia a członem równoległoboku, Xp, yp, z_P - współrzędne przemieszczenia członu roboczego [59]

wania robota powinien wykonywać obliczenia możliwie szybko, gdyż jest to konieczne do uzyskania odpowiedniej płynności działania robota - obliczenia muszą więc być względnie nieskomplikowane. Trzeba zauważyć, że w powyż. szym rozumowaniu rozdzielono orientację w przestrzeni od pozycjonowania ramienia, co bardzo upraszcza osiągnięcie właściwego rozwiązania.

Obszerniejsze i dokładniejsze informacje dotyczące zagadnienia kinema* tyki manipulatorów znajdzie Czytelnik w pozycjach literatury [12, 24, 61, 881. W celu opisania przemieszczeń, prędkości i przyspieszeń układów kinematycz-nych, wykonujących złożone ruchy w przestrzeni, stosuje się aparat matematyczny umożliwiający przede wszystkim efektywne obliczenia. Pod tym wzglę. dem najwłaściwsze zastosowanie rachunku macierzowego, który umożliwia w jednolity i zwarty formalnie sposób przedstawić geometryczne, kinematyczne i dynamiczne związki między członami manipulatora i obiektami manipulacji oraz algorytmy sterowania.

4.3. Kinematyka robotów o strukturach równoległych

4.3.1. Kinematyka manipulatora równoległego typu DELTA

Na rysunku 3.39 pokazano strukturę kinematyczną manipulatora równoległego (tripoda) typu Delta.

Zadanie proste manipulatora równoległego typu DELTA polega na wyznaczeniu pozycji członu roboczego określonej współrzędnymi: xp, yp, zp, które są funkcją trzech zmiennych konfiguracyjnych: Rg Uff || Schemat manipulatora typu DELTA opisujący wielkości geometryczne przedstawiono na rys. 4.14.

Niech Qi (i i 1,2,3) oznacza punkt w przestrzeni, powstały na skutek przesunięcia punktu 1 równolegle do wektora B_tV (linia przerywana), przy czym VQi 11 [59]. Podstawą wyznaczenia współrzędnych || yp, zp jest znalezienie współrzędnych geometrycznych || || 9 teoretycznego punktu U leżącego na prostej prostopadłej do płaszczyzny wyznaczonej przez punkty B\, m H członu roboc7^gpa||PPB^Wl^^«znacza się w przestrzeni jako

symetrii odcinka Q\Qi,

/r₂-płaszczyzny symetrii odcinka Q\Qi oraz ą - płaszczyzny punktów Q„ rozważając układ zamknięty złożony z trzech ramion robota przedstawionych na rys, 4.14 Korzysta się z postaci ogólnej równania płaszczyzny wyznaczonej przez dowolny punkt na niej leżący oraz współrzędne dowolnego wektora normalne- 101