HPIM0797

4. Wprowmiienle do kinematyki robotów

go. Zgodnie z tym, opierając się na współrzędnych punktów .v&, \'q, . -y, (/* J 2, J)_t wyznacza się równania płaszczyzn *r\ i /q leżących na punktach oJcr_c1 Słonych jako Spodki symetrii odcinków Q\Qi i Q\Q* oraz prostopadłych d₀ wektorów QtQ}*OtOi utworzonych przez te odcinki. Równanie płaszczyzny można wyznaczyć np. opierając się na współrzędnych punktu Q\ oraz współ. I rzędnych wektora normalnego wyznaczonych przez iloczyn wektorowy postaci; i QtQi    •

	Aby otrzymać współrzędni
	wiązać układ równań utworzony
i	postać ogólna jest następująca
	fAiX + B\y 4* C\Z 4* D\ ^= 0
	JA2x *b: B2y + C2z + D] » 0
w	1AyX 4* Bjy 4* CyZ 4- Dy ® 0

(4.31)

gdzie

Dt ^m —Ai.rą — Biyą — C/io,

przy czym m M C_t - są współrzędnymi wektora normalnego, a x_Ql ,yo ,zo ^sfl współrzędnymi geometrycznymi wspólnymi z płaszczyzną.

Rozwiązaniem układu równań będą współrzędne geometryczne xu_t yu* ^zv punktu U

(Bys - Dyq)A\ — (B,D₂ — B₂D\)Ay (-ByrIC₂q)A\ ~(QB₂-C₂B_t)A₃ rz_u+s

yu ww

%

(4.32)

Biv_u 4*C\~u D\

gdzie współczynniki q, r, | są określone równaniami B₂-B,A₂

(4.33)

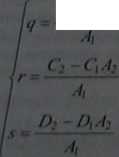
Mając współrzędne geometryczne xu, yu, m punktu U, można wprost okre

ślić położenie cbwytaMĘ

). Punkt V leży na prostej pro-

_lop_0tj|ej do /ry i przechodzącej przez punki U_% co wynika z geometrii mecha-jjęrwUi jakim joft munipulntor o strukturze zamkniętej. Odległość QjV = /j, VP ~ /j. ponieważ trójkąt QzUl^/ jest prostokątny, więc przesunięcie punktu U do P moż-nn wyznaczyć według wzoru

(jmlJPm yjlj -(Q₂U)²    (4.34)

Rozwiązanie zadaniu odwrotnego manipulatora typu DELTA polega na wyznaczeniu zmiennych konfiguracyjnych a_t (/ = I, 2, 3) jako funkcji pozycji j orientacji członu roboczego. Dla każdego ramienia manipulatora przyjmuje się układ współrzędnych X\ Y\ Z\ przy czym oś Z jest prostopadła do osi z głównego układu współrzędnych, a oś X' pokrywa się z osią siłnika napędzającego fozpatrywnne ramię. W nowym układzie współrzędnych każdego ramienia wyznacza się współrzędne punktu Bi w zależności od współrzędnych punktu P(x_P% y_P, z_P) według wzorów

. J j Xg\ =Xp + R_B ~~ R A

|Sj    (4.35)

Hj ^B *p — h

Współrzędne punktu Bi można wyrazić również w funkcji kątów a_i% Ą, y*

& = l\ COS£?| — I2 COS^j COS P\

*-ya\ «/2sin^i    (4.36)

z$\ = l\ sin cc\ + h sin P\

Z powyższych zależności wyznacza się kąty

i

(4.37)

₌ arcsin^

%

|    (l\GO&Ct\-XB\

B\ = arccos -

4 I /acosn

Wiedząc, że kąt    kątem dopełniającym do (ał+ $) w płaszczyźnie

ramienia, można go wyznaczyć wg wzoru

i i arc tg ^-1    (4J8)

103