HPIM0790

4- Wprowadzenie do kinematyki robotów

- w przypadku ruchów obrotowych (A, B,C) w kierunku prawoskrętny^ uwzględniając dodatni zwrot odpowiadających im osi układów waW rzędnych X, Y, 1.

5.    Układy osi współrzędnych dwóch pozostałych części struktury kij,, matycznej, występujących w mechanizmie, a mianowicie lokalnej i globalnej, _s identyczne, jeśli chodzi o kierunek i zwrot osi z układem podstawowym i zwją zane odpowiednio z ostatnim zespołem lokalnego lub globalnego odcinka łafe, cha kinematycznego mechanizmu.

6.    Zespoły mchu - człony mechanizmu - oznacza się dużymi literami v | Z, A, B, C odpowiednio do oznaczeń osi współrzędnych i rodzaju ruchu i d_0>' daje indeks |»i (np. Q, w zależności od odcinka łańcucha kinematycznego w którym występują.

7.    Syntetyczny zapis struktury łańcucha kinematycznego mechanizmu ro. bota jest uporządkowanym zbiorem oznaczeń występujących w nim zespołów mchu; zbiór rozpoczyna pierwszy po podstawie, a kończy ostami przed chwyta, kiem lub narzędziem zespół mchu mechanizmu.

8.    Wielokrotność występowania zespołu mchu danego rodzaju w tym sa-mym odcinku łańcucha kinematycznego rozróżnia się przez numerowanie, a krotność łańcucha w obrębie całego mechanizmu lub jego wybranej części i przez zapis równoleglo-szeregowy.

Przykłady tworzenia układów odniesienia wraz ze wskazaniem ruchów liniowych i obrotowych przedstawiono na rys. 4.2. Ruchy p 1 Z określono jako przesunięcia liniowe, mchy A,B,C- jako obrotowe względem poszczególnych osi.

a)    b) II .....    ■ _c).

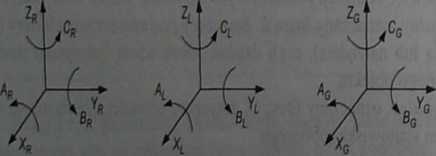
Rysunek4.2    j ... _

Układy odniesienia robota przemysłowego: a) regionalny, b) lokalny, c) globalny

Wykorzystując pokazane układy odniesienia (rys. 4.2) oraz schemat kinematyczny robota, zapis jego struktury można przedstawić w postaci symbolicznej. Na rysunku 4.3 zilustrowano zasadę zapisu struktury robota o strukturze kinematycznej Kg S B B Q, Bi). Pierwszym członem zapisu struktury kinematycznej jest zespół / ruchu regionalnego (C/?j), ostatnim członem - ze-88 spół | ruchu lokalnego (#/.).

Rysunek 4.3_________

Określenie podstawowego układu osi współrzędnych, kierunków ruchu i zapisu struktury mechanizmu robota; 1 - podstawa, 2 - zespól ruchu, i - sprzęg chwytaka

Tak przedstawiony zapis umożliwia wskazanie: liczby stopni swobody, układu współrzędnych ruchów regionalnych ramienia oraz możliwości kinematycznych robota. O przynależności zespołu ruchu do części globalnej, regionalnej lub lokalnej mechanizmu jednostki kinematycznej rozstrzyga konstrukcja (geometria) członu oraz mechanizm przemieszczeń. Dla znacznej części rozwiązań granicę poszczególnych odcinków ruchu wskazuje producent.

Podstawowy układ osi współrzędnych jest związany z mechanizmem jednostki kinematycznej robota (stąd nazwa układ maszynowy) i zmienia swe położenie wraz z przemieszczaniem członów mechanizmu. Aby określić te przemieszczenia, a wynikowo przemieszczenia chwytaka lub narzędzia robota, wprowadza się dodatkowy układ osi współrzędnych, związany z przestrzenią stanowiska roboczego, w którym jest osadzona jednostka kinematyczna (układ odniesienia). W pracy [67] proponuje się, że osie układu odniesienia i układu maszynowego powinny pokrywać się w normalnym (katalogowym) położeniu członów łańcucha kinematycznego mechanizmu robota.    89