skrypt'

Filtracja innowacyjna i mooelowanie s tochastyczne sygnałów

> biały szum

' MO

Rys. 4.13. Globalna realizacja ortogonalna filtru modelującego

4.3. Rotacje hiperboliczne i kołowe

Przyjmijmy, źe współczynnik Schurn p, to tangens hiperboliczny pewnego kąta Yi

Pi = tgl> H'i

(4 50)

Wówczas sekcja elementarna 0(p,j (4.20) filtru innowacyjnego przyjmuje postać

_ Tcosli Yi sinh i/r, 1 'P'' ^— [sinhig, coshę/,J

(4.51)

Zatem każdą sekcję filtru innowacyjnego możemy interpretować jako rotację hiperboliczną o kąt yr, wektora unormowanych sygnałów wejściowych e, | (r) i r₍_i(r- I) tej sekcji Biorąc pod uwagę, że |p,| < 1, przyjmijmy, że

flpjgsinęy    (4 52)

Wówczas sekcję elementarną <j(pi) (4 46) filtru modelującego możemy przedstawić jako

cos <p, ^a(P') sin tp,

- sin <Pi cos <p,

(4 53)

Stąd wniosek, że każdą sekcję filtru modelującego możemy interpretować jako rotację kołową o kąt tp, wektora unormowanych sygnałów wejściowych e,(t) i r,_i(r — I) tej sekcji Ponieważ operacja rotacji (obrotu) jest operacją niezmienniczą ze względu na długość przekształcanych wektorów (jest to operacja ortogonalna), stąd wniosek, że algorytm zarówno filtru innowacyjnego, jak i modelującego charakteryzuje się samorzutną stabilnością numeryczną

_—»vui.aiE i KOŁOWE

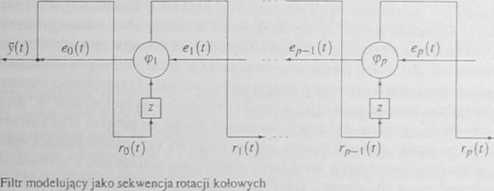
Sekcję elementarną filtru innowacyjnego, opisaną rotacją hiperboliczną (4.51), można więc schematycznie przedstawić na rys. 4.14, zaś sekcję elementarną filtru modelującego, opisaną rotacją kołową (4.53) - na rys. 4 15 Zatem stmkturę kaskadową filtru innowacyjnego z. rys. 3 10 możemy obecnie przedstawić na rys. 4 16 za pomocą sekwencji rotacji hiperbolicz.nych Podobnie, strukturę kaskadową filtru modelującego z rys 4 12 możemy zinterpretować jako sekwencję rotacji kołowych (patrz. rys. 4 17). Na zakończenie zauważmy, że zarówno rotacje hiperboliczne, jak i rotacje kołowe mają dogodną realizację sprzętową

za pomocą tzw, procesora CORDIC [50. 471 (od COordinale Rotation Digital Computer).

n(0

MO —I Vr+i    e„₊|(r)

M'- O

RYS 4 |4 Rotacja hiperboliczną

r»+l(0

^rn(t~ 1)

Rys 4 |5 Rotacja kołowa

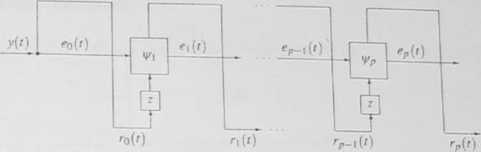
Rys 4 16 Filtr innowacyjny jako sekwencja rotacji hiperbolicznych

108

((((lIIISSBSliBll

Filtracja innowacyjna i modelowanie stochastyczne sygnałów

4.4. Ortogonalna parametryzacja sygnałów drugiego rzędu

Z dotychczasowych rozważań w niniejszym rozdziale wynika. Ze znajomość współczynników Schura

(Pt. - • .Pp}

(4.54)

obserwowanego sygnału y jest wystarczająca do przeprowadzenia ortogonalnej cyfrowej syntezy (modelowania stochastycznego) tego sygnału Wyznaczanie zbioru tych współczynników nazywa się zaz.wyczaj parametryzacją sygnału y.

Z poprzednich rozdziałów wynika, że istnieje kilka równoważnych metod parametryzacji sygnału, prowadzących do wyznaczenia tego samego zbioru współczynników Schura (zależnych od tego, jakimi dysponujemy informacjami odnośnie do parametryzowanego sygnału). I tak:

• Jeśli dane są obserwacje sygnału y. tj. zbiór zmiennych losowych {y(r), y(r - 1),.. .,y(t - p)}. to współczynniki Schura tego sygnału można wyznaczyć na podstawie zależności (3.3) jako

Pi = -(«!-1 (0,n-\(t - 1))u= -Ee,-1 (i)D- |(Z - I)

(4.55)

Współczynniki te interpretujemy wówczas jako korelacje wzajemne unormowanych błędów prognozy w przód i w tył Jeśli zamiast zmiennych losowych obserwacje sygnału stanowi nabór próbek {yo.....yr}. to wyznacza się esty

matory współczynników Schura (estymatory korelacji wzajemnych wektorów próbek błędów w przód i w tył)

4.5.

109

_uniowegq ...........

Dla ergodycznego sygnału y mamy wówczas

A = lim Ip,r

(4.5

Do zagadmema tego. zw.ązanego z efektywnymi algorytmami parametryza szeregów czasowych i nastawionego na ,ch realizację w czasie rzeczywisty cyjnej'^C'^m> *    ⁶' ^doty^cz4cym cyfrowej ortogonalnej filtracji adapi

• Jeśli punkt wyjścia stanowi funkcja kowariancji {c(0),c(l),.. ,c(p sygnału y (luh jej estymator wyznaczony na podstawie naboru prób, {>’0i    i yr}), to współczynniki Schura można wyznaczyć z zależności (2.30

Pi = "([4,-1 OJ,[0B,.,])_c =

= -[4,-1 0jc,[0=

= -[a,_ i.o - - - u,-1,-, 00... OjCpfO i,-1.,-1... 0₍-10 0... 0)' =

= ~[ll^ei-1II0... 0 df. i,₁₊1...d,_ _{t p}] x

x[0*i-i,/-_l...*i__lt00...0]' =

4-1,1

- --- (4.58;

Si— I I

gdzie g,(i) = oznacza normę (2.192). Jak widać, la metoda parametryzacji jest identyczna z algebraiczną wersja algorytmu Schura. przedstawioną w punkcie 2.2.5 (patrz Przykład 7.3 w rozdziale 7).

• Jeśli jest dana widmowa gęstość mocy sygnału y (lub jej estymator), to parametryzację sygnału możemy przeprowadzić na podstawie zależności (2.276)

Pt = - (4,-, (z).zB,., (z))„ = £    W(e>^e)e-^IBB,-i M⁹) ^ (4-59)

W kolejnym podrozdziale wykorzystamy omówione dotąd wyniki, stanowiące podstawę do realizacji systemów cyfrowej transmisji sygnałów tzw. metodą liniowego kodowania prognozującego, z kompresją ilości przesyłanej informacji.

Cyfrowa transmisja sygnałów metodą liniowego kodowania prognozującego

Jako przykład wykorzystania przedstawionych w niniejszym rozdziale algorytmów ortogonalnej parametryzacji i modelowania sygnałów 2-go rzędu może służyć metoda transmisji sygnałów cyfrowych, zwana metodą tzw. liniowego

(4.56)

■^i- i.r][0 r,_ i.o ■ ■ n-i ,r-i]'

gdzie c/., oraz rij stanowią próbki sygnałów błędów prognozy w pizód i w tył, transmitowanych w strukturze filtru (patrz Przykład 7.3 w rozdziale 7).

Pi,T = l«i—1.0-

111

110