str009

Rachunek koni rolujemy, wyznaczając bh|d indeksu z obili/ouyclt odczytów M i (90°00'09,5" + 270°00'09,5"    160”)    0.5"

jak być powinno.

Chcąc ustawić w poziomie oś celową tego teodolitu należy /grać obrazy końcowi pęcherzyka libeli kolimacyjnej, pokrętką mikrometru nastawić końcówki odczytów I

przy KL — 90°00'09,5" przy KP — 270°00'09,5"

i doprowadzić do koincydencji, posługując się leniwką ruchu pionowego.

Załóżmy teraz, że oś celową tego samego instrumentu chcemy ustawić pod kątem 7    -.112' 18". Jakie odczyty odpowiadają temu położeniu osi celowej?

< )blic/ymy odczyty R_L, R_P koła zrektyfikowanego, odpowiadające danemu kątowi < przy obu położeniach koła. Z zależności

a = 90" - R_l a = R_P - 270°

oii/vmu|ciuy

R, 90° - a = 90° - ( — 3° 12'18") = 93°12'18"

Kp » 270” + a = 270° + (-3° 12'18") = 226°47'42"

' •> |n' po/mda obliczyć odczyty koła niezrektyfikowanego z równania błędu indeksu O, R, + M = 93° 12'18"+ 9,5" = 93°12'27,5"

Op Rp + M = 266^c47'42" + 9,5" = 226°47'51,5" l ......... |r w opisany wyżej sposób.

U PRZEKRÓJ NORMALNY I JEGO ELEMENTY

1.3.1. PODSTAWOWE POJĘCIA I OZNACZENIA

Niwelacją trygonometryczną nazywamy konstrukcję geodezyjną, umożliwiającą wyznaczenie wysokości punktów na podstawie pomierzonych kątów pionowych x^ub oraz długości, które mogą być pomierzone albo obliczone.

Za powierzchnię odniesienia, względem której oblicza się wysokości punktów, przyjmiemy powierzchnię kuli o promieniu R = 6 382 km (średni promień krzywizny elipsoidy Krassowskiego dla naszych szerokości). Kulę tę nazwiemy kulą odniesienia. Hędziemy przy tym zakładać, że linia pionu wystawiona w dowolnym punkcie na powierzchni Ziemi przechodzi przez środek O kuli odniesienia, natomiast powierzchnia odniesienia pokrywa się ze średnim poziomem morza. Wysokości będziemy liczyli wzdłuż linii pionów.

Jeśli założymy, że oś pionowa teodolitu ustawionego centrycznie nad punktem P pokrywa się z linią pionu punktu P, to punkt centralny I stanowi przecięcie osi obrotu lunety (osi poziomej), osi celowej oraz linii pionu punktu P.

Płaszczyzną horyzontu nazwiemy płaszczyznę poziomą, przechodzącą przez punkt centralny I. Płaszczyzna horyzontu jest prostopadła do linii pionu punktu I*.

1'h'Mi i z.clini:| horyzontu un/winm pnwicrz.ehnię kuli koncentrycznej z kuli) li.....ii nln i przechodzącą przez punki n iilinlny I.

I< miiimii I',, punktu I* na piwn i -i Imię odniesienia nazywamy punki przecięcia

i ni punk lu I* z powierzchnię odniesieniu Analogicznie zdefiniujemy rzut K„ punktu i imwi/uiy, że rzutowanie odbywa się po liniach pionów, których zbieżność limitu ir O założyliśmy. Nie są to więc rzuty równoległe.

I* im ni odcinak PK na powierzchnię odniesienia nazwiemy łuk koła o promieniu i .....II. u o, ograniczony punktami P_L„ K.₀.

¹ u., Imj tri li znajduje się na wysokości w nad punktem geodezyjnym K. K;|l ,ot u h między odcinkiem IE oraz jego rzutem na płaszczyznę horyzontu nazwiemy i o. ni |in mowym i oznaczymy symbolem a. W ten sposób będziemy zawsze oznaczali i >|iy t twrliininowanym wpływem refrakcji.

I p pionowy obserwowany oznaczymy symbolem a°t>. Jest to kąt obarczony pb ui ni refrakcji.

Pi ,| lujem normalnym nazwiemy przekrój kuli odniesienia płaszczyzną przc-ln ul i|. ,| przez środek O. Dalej będą nas interesować przekroje normalne zawierające i mil i 11 ul ruiny I oraz punkt celu E. Przekrój normalny pokazano na rys. 1.8, gdzie o ........ni główne jego elementy:

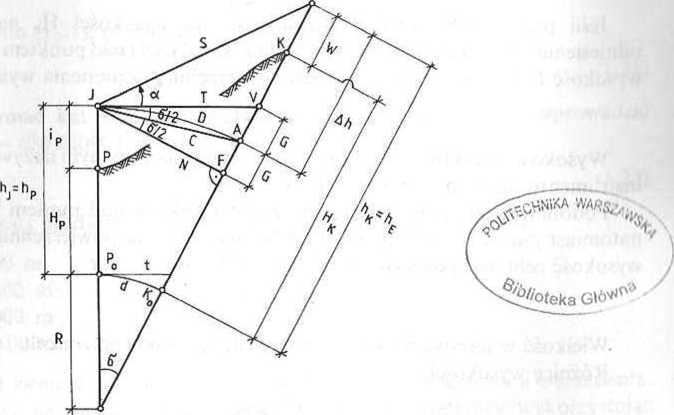
o

Rys. 1.8.

długość odcinka IE prostej łączącej punkt centralny 1 z celem E, nazywana długością skośną. Otrzymujemy ją np. z pomiaru dalmierzem po wprowadzeniu poprawek instrumentalnych i poprawki atmosferycznej,

I długość odcinka IV leżącego na płaszczyźnie horyzontu. Punkt V jest punktem przebicia płaszczyzny horyzontu linią pionu punktu geodezyjnego K. Odcinek